Question

A body revolving with a uniform speed $v$ in a circle of radius $r$. The angular acceleration of the body is
\[\begin{align}
  & \text{A}\text{.}\dfrac{\text{v}}{\text{r}} \\
 & \text{B}\text{.0} \\
 & \text{C}\text{.}\dfrac{{{\text{v}}^{\text{2}}}}{\text{r}}\text{ along the radius and towards the centre} \\
 & \text{D}\text{.}\dfrac{{{\text{v}}^{\text{2}}}}{\text{r}}\text{ along the radius and away from the centre} \\
\end{align}\]

Answer 1

Hint: In circular motion centripetal force is perpendicular to velocity. Also if the particles decrease or increase their speeds in circular motion then acceleration is generated which deviates the net acceleration from pointing towards the centre.
Formula: $a=\dfrac{v^{2}}{r}$

Complete answer:
We know that the motions are two types: one is straight motion and the circular motion. Then we know that circular motion, though the magnitude of velocity is a constant, the direction of velocity is changing. A circle. It is also defined as rotation of an object along a circular path. It can be of two forms, uniform circular motion, with constant angular rate of rotation and constant speed, or non-uniform circular motion with a changing rate of rotation.
Consider a body of mass $m$ moving along the circumference of a circle. the radius of a circle $r$ with velocity $v$,as shown in the figure. Then if a small force $F$ is applied on the body , then we know that the force is given as $F=ma$.

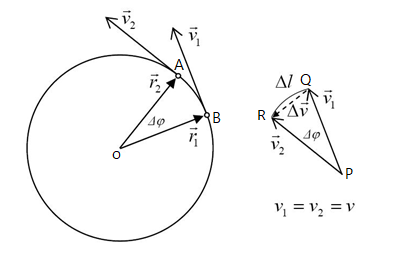
Where, $a$ is the acceleration and is given as the rate of change of velocity $\Delta v$ with respect to time.
Then, the acceleration due to centripetal force is given by,x$a=\dfrac{v^{2}}{r}$. Clearly as the velocity $v$ and the radius $r$ of the circle are constant, acceleration $a$ will also remain a constant. Clearly, angular acceleration points towards the centre.

Hence the correct answer is option \[\text{C}\text{.}\dfrac{{{\text{v}}^{\text{2}}}}{\text{r}}\text{ along the radius and towards the centre}\]

Note:
We know that angular velocity $\omega$ is defined as the rate at which the angular position varies with respect to time, and also given as $\omega=\dfrac{v}{r}$ where $v$ is the linear velocity and $r$ is the from between the centre of the circle and the position of the body. Whereas, angular acceleration $\alpha$ is the change in angular velocity with respect to time.