
A body projected upwards with a velocity $u$. It passes through a certain point above the ground after $t_{1}$ seconds. The time after which the body passes through the same point during the return journey is
\[\begin{align}
& A.\dfrac{u}{g}-t_{1}^{2} \\
& B.2\left[ \dfrac{u}{g}-{{t}_{1}} \right] \\
& C.3\dfrac{{{u}^{2}}}{g}-{{t}_{1}} \\
& D.3\dfrac{{{u}^{2}}}{{{g}^{2}}}-{{t}_{1}} \\
\end{align}\]
Answer
591.6k+ views
Hint: A body which is moving upward, is said to experience free fall, if only force due to gravity is acting on the body. Here, since there is no external force on the body, the body experiences free fall. Where only acceleration due to gravity is acting on the body.
Formula used:
$v=u+at$
Complete answer:
When the body is projected vertically upward, it will experience acceleration due to gravity $g$
Let us assume that there is no external force on the body, except the force of gravitation.
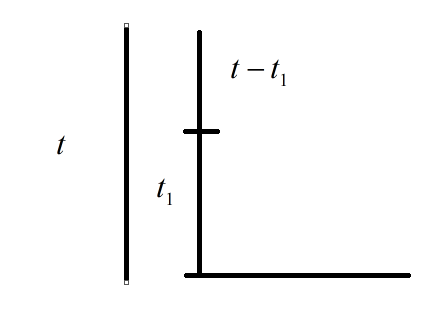
Let the total time taken by the body projected be $t$.
Since the initial velocity of the body is $u$, then the final velocity, $v=0$ as the body will come to stop.
Then, from $v=u+at$, we get
$v=u-gt$
Or $u=gt$
Or, $t=\dfrac{u}{g}$
Let the time taken by the body to pass the point is $t_{1}$
Then the time taken by the body after crossing the point will be $t-t_{1}=\dfrac{u}{g}-t_{1}$
Since the body crosses this point twice, once during the upward motion and the other during its downward motion, due to free fall of the body.
We can say that the time taken after which the body passes through the same point during the return journey is $2\left[\dfrac{u}{g}-t_{1}\right]$
Hence the answer is $2\left[\dfrac{u}{g}-t_{1}\right]$
So, the correct answer is “Option B”.
Note:
Acceleration due to gravity $g$ has a negative sign, as it tends to draw the ball towards the earth. Free fall results in weightlessness, where the mass of the body does not affect the motion of the body. Thus, you may notice that the mass of the body is not given here.
Formula used:
$v=u+at$
Complete answer:
When the body is projected vertically upward, it will experience acceleration due to gravity $g$
Let us assume that there is no external force on the body, except the force of gravitation.
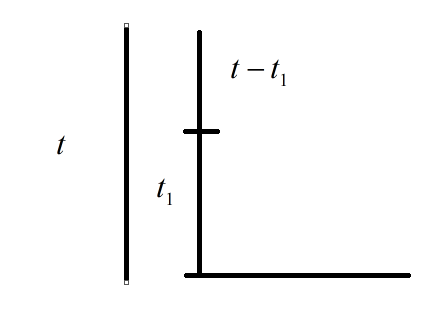
Let the total time taken by the body projected be $t$.
Since the initial velocity of the body is $u$, then the final velocity, $v=0$ as the body will come to stop.
Then, from $v=u+at$, we get
$v=u-gt$
Or $u=gt$
Or, $t=\dfrac{u}{g}$
Let the time taken by the body to pass the point is $t_{1}$
Then the time taken by the body after crossing the point will be $t-t_{1}=\dfrac{u}{g}-t_{1}$
Since the body crosses this point twice, once during the upward motion and the other during its downward motion, due to free fall of the body.
We can say that the time taken after which the body passes through the same point during the return journey is $2\left[\dfrac{u}{g}-t_{1}\right]$
Hence the answer is $2\left[\dfrac{u}{g}-t_{1}\right]$
So, the correct answer is “Option B”.
Note:
Acceleration due to gravity $g$ has a negative sign, as it tends to draw the ball towards the earth. Free fall results in weightlessness, where the mass of the body does not affect the motion of the body. Thus, you may notice that the mass of the body is not given here.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




