Question

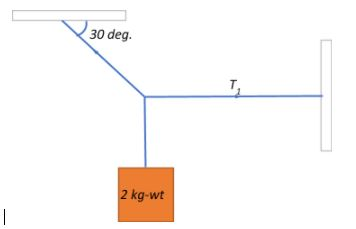
A body of weight $2\;kg$ is suspended as shown in the figure. The tension $T_1$ in the horizontal string (in kg wt) is ?

Answer 1

Hint: Begin by resolving the tension in the inclined string into its horizontal and vertical components. Then, by treating this as a free-body diagram, determine the equation(s) of balancing forces at systemic equilibrium. Once you get expressions of the horizontal and vertical components of this tension, one of which will be in terms of the horizontal tension.
Then, you can use the fact that the angle made by the inclined string is equivalent to the angle between the resultant tension acting on this part of the string and its horizontal component since they are geometrically alternating angles, and evaluate the equilibrium equations. This will consequently lead you to the appropriate result.

Formula used:
Resultant tension in the string $T^2 = (Tcos\theta)^2 + (Tsin\theta)^2$

Complete step-by-step answer:
We know that both the horizontal and the inclined string experience a tension in their structure owing to the $2\;kg.wt$ suspended tautly from them.
The inclined string experiences a resultant tension in the structural direction of the string as a result of the tension in the horizontal string and the suspended weight.
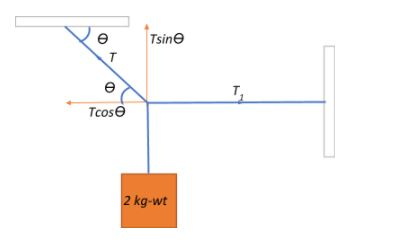
We can begin by resolving the tension in the inclined string in order to determine its directionally-specific influencing components. Let the resultant tension in this part of the string be T.
At equilibrium, the component of this tension T balancing out the tension $T_1$ in the horizontal part of the string is given as:
$Tcos\theta = T_1$
The component of T acting to balance out the weight of the body can be given as:
$Tsin\theta = 2$

Given that $\theta = 30^{\circ}$:
$Tsin(30^{\circ}) = 2 \Rightarrow T.\dfrac{1}{2} = 2 \Rightarrow T = 4\;kg.wt$
From the first equation, we have:
$Tcos(30^{\circ}) = T_1 \Rightarrow 4.\dfrac{\sqrt{3}}{2} = T_1$
$\Rightarrow T_1 = 2\sqrt{3} = 2 \times 1.732 = 3.46\;kg.wt $
Therefore, the tension in the horizontal string is found to be equal to $\approx 3.5\;kg.wt $

Note: Remember to always consider only those components of the influencing force that contribute to the system in the considered direction, while bringing about the resolution of vectors into their horizontal and vertical components. This is the principle on which our analysis of the problem is based and helps us account for only directionally-specific contributions.