Question

A body of weight \[200N\] is suspended with the help of string as shown in the figure. Find the tensions in the strings.

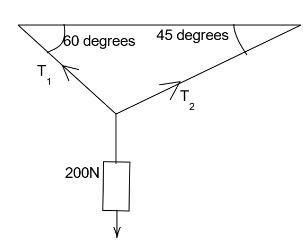
Answer 1

Hint: We are asked to find the tension in the strings. We can start by resolving the tension in the strings into their respective sine and cosine components. Then we can find the values that are equal and equate them with one another. This gives us the relationship between the tensions of the two strings. We have two components of each tension and this gives us two equations and two unknown values. We can solve this and get the values of tension of the two strings.

Complete step by step answer:
We can resolve the value of the tension in each string as
The x-component of the tension in the first string is, \[{T_x} = {T_1}\cos 30\]
The y-component of the tension in the first string is, \[{T_y} = {T_1}\sin 30\]
The x-component of the tension in the second string is, \[{T_x} = {T_2}\cos 45\]
The y-component of the tension in the second string is, \[{T_y} = {T_2}\sin 45\]
Free body diagram for the body is as follows:

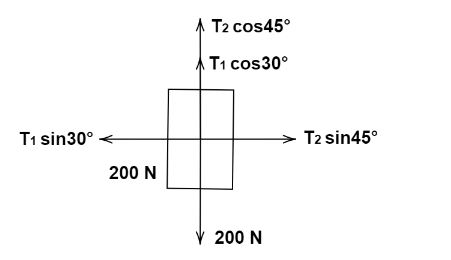
At equilibrium, the x-components of the two tensions will be equal
\[{T_1}\cos 30 = {T_2}\cos 45\]
Substituting the values, we get a relationship between the tension values we get,
\[\dfrac{1}{2}{T_1} = \dfrac{1}{{\sqrt 2 }}{T_2}\]
We can cross multiply and get, \[\sqrt 2 {T_1} = 2{T_2}\]

Now we can move onto finding a relationship between the sine components of the two vectors.
\[{T_1}\sin 60 + {T_2}\sin 45 = 200\]
As the cosine components are responsible for the mass of the block. Now, we can substitute the value of one of the tension with respect to the other and get
\[\sqrt 2 {T_2} \times \dfrac{{\sqrt 3 }}{2} + {T_2}\dfrac{1}{{\sqrt 2 }} = 200\]
We can solve this and get the value of \[{T_2}\] as,
\[{T_2} = \dfrac{{200\sqrt 2 }}{{\left( {\sqrt 3 + 1} \right)}}\]
We can substitute this value in the relationship we got and get the value of the tension of the first string as,
\[{T_1} = \dfrac{{400}}{{\left( {\sqrt 3 + 1} \right)}}\]

Therefore, the tension in the strings are $\dfrac{{400}}{{\left( {\sqrt 3 + 1} \right)}}$ and $\dfrac{{200\sqrt 2 }}{{\left( {\sqrt 3 + 1} \right)}}$.

Note: Vectors can be split into two components, the sine and cosine components.
For instance, tension is split into two components, the x-component will be \[{T_x} = T\cos X\]. The y-component will be \[{T_y} = T\sin X\].