Question

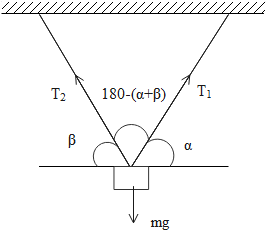
A body of mass m is suspended by two strings making angles\[\alpha \] and\[\beta \] with the horizontal. Tensions in two strings are

\[\begin{align}
  & A.\,{{T}_{1}}=\dfrac{mg\cos \beta }{\sin (\alpha +\beta )}={{T}_{2}} \\
 & B.\,{{T}_{1}}={{T}_{2}}\dfrac{mg\cos \beta }{\sin (\alpha +\beta )} \\
 & C.\,{{T}_{1}}=\dfrac{mg\cos \beta }{\sin (\alpha +\beta )},\,{{T}_{2}}=\dfrac{mg\cos \alpha }{\sin (\alpha +\beta )} \\
 & D.\,\text{None}\,\text{of}\,\text{these} \\
\end{align}\]

Answer 1

Hint: The horizontal components of the tensions balance each other when the body will be in equilibrium. Similarly, the vertical components of the tension balance the weight of the body. So, using these conditions, we will find the expressions for the same and will compute the expressions for the tensions.

Complete answer:
Firstly we will consider a diagram representing the directions of the horizontal and vertical components of the tension working on the string.

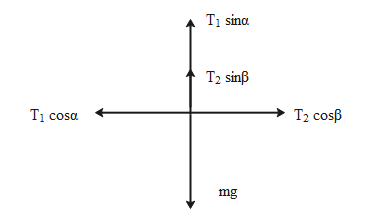
The horizontal components of \[{{T}_{1}}\]and \[{{T}_{2}}\]balance each other as the body is in equilibrium.
\[{{T}_{1}}\cos \alpha ={{T}_{2}}\cos \beta \]
\[{{T}_{2}}=\dfrac{{{T}_{1}}\cos \alpha }{\cos \beta }\]…… (1)
The vertical components of \[{{T}_{1}}\]and \[{{T}_{2}}\]balance the weight of the body.
\[{{T}_{1}}\sin \alpha +{{T}_{2}}\sin \beta =mg\]…. (2)
Substitute the equation (1) in equation (2).
\[\begin{align}
  & {{T}_{1}}\sin \alpha +\dfrac{{{T}_{1}}\cos \alpha }{\cos \beta }\sin \beta =mg \\
 & \Rightarrow {{T}_{1}}=\dfrac{mg\cos \beta }{\sin \alpha \cos \beta +\cos \alpha \sin \beta } \\
\end{align}\]
Using the trigonometric function, continue further computation.
\[{{T}_{1}}=\dfrac{mg\cos \beta }{\sin (\alpha +\beta )}\]
The trigonometric function that we have used to solve the above equation is given as follows.
\[\sin (a+b)=\sin a\cos b+\sin b\cos a\]
Thus, the tension in the first string is, \[{{T}_{1}}=\dfrac{mg\cos \beta }{\sin (\alpha +\beta )}\].
Consider the equation and substitute the expression of tension in the first string.
\[\begin{align}
  & {{T}_{2}}=\dfrac{mg\cos \beta }{\sin (\alpha +\beta )}\dfrac{\cos \alpha }{\cos \beta } \\
 & \therefore {{T}_{2}}=\dfrac{mg\cos \alpha }{\sin (\alpha +\beta )} \\
\end{align}\]
Thus, the tension in the second string is, \[{{T}_{2}}=\dfrac{mg\cos \alpha }{\sin (\alpha +\beta )}\].
Therefore, the tensions in the string are: \[{{T}_{1}}=\dfrac{mg\cos \beta }{\sin (\alpha +\beta )}\]and \[{{T}_{2}}=\dfrac{mg\cos \alpha }{\sin (\alpha +\beta )}\].
\[\therefore \] The tensions in the strings are \[{{T}_{1}}=\dfrac{mg\cos \beta }{\sin (\alpha +\beta )}\]and \[{{T}_{2}}=\dfrac{mg\cos \alpha }{\sin (\alpha +\beta )}\].

Thus, option (C) is correct.

Note:
The solution to this problem completely depends on the diagram representing the directions of the horizontal and vertical components of the tension working on the string. So, the tension in the string is divided into horizontal and vertical components. In the case of horizontal components, they balance each other, whereas, in the case of vertical components, they get balanced by the weight of the string.