Question

A body of mass 2kg slides down with an acceleration of 3m/s$^2$ on a rough inclined plane having a slope of 30$^\circ $. The external force required to take the same body up the plane with the same acceleration will be: (g = 10m/s$^2$)
A. 4N
B. 14N
C. 6N
D. 20N

Answer 1

Hint:We solve this question in two cases, first when the body slides down and second when the body slides up the inclined plane. Draw the free body diagram in both the cases and write Newton's law of motion equation of force. By using the values obtained in the two cases we can find the desired result.

Complete step by step answer:
Given, the mass of the body, m$ = 2kg$. Acceleration of the body, $a = 3m/{s^2}$.
Inclination of inclined plane,$\theta = 30^\circ $. Let us consider two cases.
Case 1: when the body slides down the inclined plane.Drawing the free body diagram.

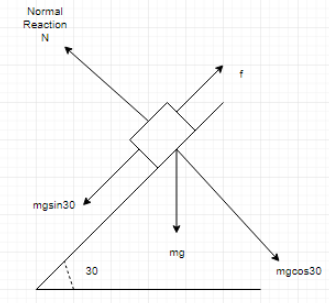
Writing the equation according to Newton's law of motion,
$ma = mg\sin \theta - f \\
\Rightarrow ma = g\sin \theta - \mu mg\cos \theta \\
\Rightarrow a = g\sin \theta - \mu g\cos \theta \\ $
Substituting the value of a$ = 3m/{s^2}$ and $\theta = 30^\circ $.
$3 = 10\sin 30^\circ - \mu 10\cos 30^\circ \\
\Rightarrow 3 = 10 \times \dfrac{1}{2} - \mu \times 10 \times \dfrac{{\sqrt 3 }}{2} \\
\Rightarrow 5\sqrt 3 \mu = 2 \\
\Rightarrow\mu = \dfrac{2}{{5\sqrt 3 }}$
Therefore we get $\mu = \dfrac{2}{{5\sqrt 3 }}$.

Case 2: when the body slides up the inclined plane.
Writing the equation according to Newton's law of motion,
Let the required force be F.
$F - mg\sin \theta - f = ma$
Substituting the value of m$ = 2kg,\theta = 30^\circ $and $a = 3m/{s^2}$, we get,
$F - 2 \times 10 \times \sin 30^\circ - \mu \times 2 \times 10 \times \cos 30^\circ = 2 \times 3 \\
\Rightarrow F - 20 \times \dfrac{1}{2} - \dfrac{2}{{5\sqrt 3 }} \times 20 \times \dfrac{{\sqrt 3 }}{2} = 6 \\
\Rightarrow F - 10 - 4 = 6 \\
\Rightarrow F = 6 + 14 \\
\therefore F = 20N$
Therefore we get the force as 20N.

Hence, option D is correct.

Note:We should learn to write Newton’s second law equation to solve such a type of problem.Therefore using Newton's law of motion we can write $F = ma$.While doing inclined plane problems first of all we should represent on a free body diagram all the forces acting on the block or the body. Also, to keep in mind is that frictional force always acts in the direction opposite to the motion.