Question

A body of mass $2\;kg$ has an initial velocity of $3\;m{s^{ - 1}}$ along $OE$ and it is subjected to a force of $4\;N$ along of direction perpendicular to $OE$ as shown in figure. What is the distance travelled by the body in $4\;s$ from $O$?

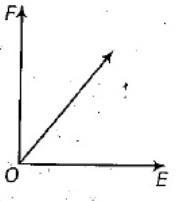
A. $12\;m$
B. $20\;m$
C. $28\;m$
D. $48\;m$

Answer 1

Hint: Initially, the body of mass $2\;kg$ has a constant velocity in the direction $OE$, by using the distance and speed relation the distance travelled by the body in the direction $OE$ can be calculated. Then a force is applied on the body along the direction $OF$. Thus, the force generates an acceleration on the body along the direction $OF$ and by using Newton's law of motion, the acceleration value is derived. And by applying the equation of motion, the distance travelled in the direction $OF$ can be calculated. Finally, using Pythagoras theorem to calculate the distance travelled by body after $4\;s$.

Useful formula:
Relation between velocity and displacement,
Displacement = Velocity * Time

Equation of motion is given by,
$S = ut + \dfrac{1}{2}a{t^2}$
Where, $S$ is the displacement, $u$ is the initial velocity, $t$ is the time taken and $a$ is the acceleration of the body.

Newton’s second law of motion is given by,
$F = ma$
Where, $F$ is the force applied on the body, $m$ is the mass of the body and $a$ is the acceleration of the body.

Given data:
Mass of the body, $m = 2\;kg$
Initial velocity of body along $OE$, ${V_{OE}} = 3\;m{s^{ - 1}}$
Force applied along $OF$, $F = 4\;N$
Time taken by the body, $t = 4\;s$

Complete Step by step solution:
The distance travelled by the body along $OE$,
${S_{OE}} = {V_{OE}} \times t$
Where, ${S_{OE}}$ is the displacement along $OE$.
Substituting the given values in above equation,
$
  {S_{OE}} = 3\;m{s^{ - 1}} \times 4\;s \\
  {S_{OE}} = 12\;m \\
 $

The acceleration of the body along $OF$ by Newton’s law,
$a = \dfrac{F}{m}$
Substituting the given values in above equation,
$
  a = \dfrac{{4\;N}}{{2\;kg}} \\
  a = 2\;m{s^{ - 2}} \\
 $

By applying equation of motion along direction $OF$,
${S_{OF}} = ut + \dfrac{1}{2}a{t^2}$
Where, ${S_{OF}}$ is the displacement along $OF$.
Substituting the given values in above equation, we get
$
  {S_{OF}} = \left( {0 \times 4} \right) + \dfrac{1}{2}\left( {2\;m{s^{ - 2}} \times {{\left( {4\;s} \right)}^2}} \right) \\
  {S_{OF}} = \dfrac{1}{2}\left( {2 \times 16} \right) \\
  {S_{OF}} = 16\;m \\
 $
Hence, the free body diagram should be,

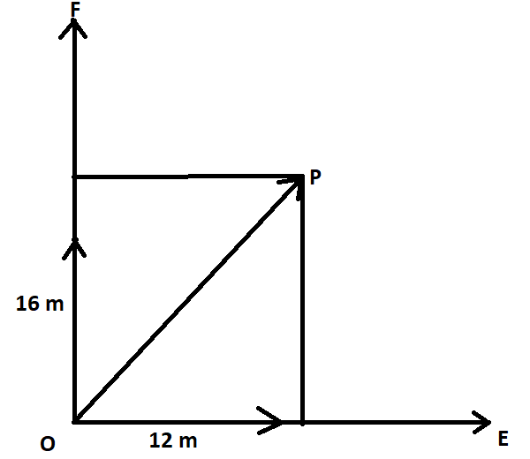
By applying Pythagoras theorem, we get
$
  {\left( {OP} \right)^2} = {\left( {12} \right)^2} + {\left( {16} \right)^2} \\
  OP = \sqrt {\left( {144 + 256} \right)} \\
  OP = \sqrt {400} \\
  OP = 20\;m \\
 $
Hence, the option (B) is correct.

Note: A body of certain mass, moving in the linear direction and then an additional force is applied on that body tends the body to move in the resultant direction of the force. Thus, the body moves along $OP$, due to the force on the two normal sides of the body.