Question

A body of mass 2 kg is moving towards the north with a speed of 4m/s. A force of 4 N is applied on it towards the west. Displacement of the body 2 seconds after the force is applied
(A) \[4\sqrt{5}m\]
(B) \[4\sqrt{2}m\]
(C) \[5\sqrt{4}m\]
(D) \[5\sqrt{2}m\]

Answer 1

Hint:Here we are given with the body of given mass moving with a given velocity (magnitude and direction both are given) and force is applied to it. We can solve this using vectors.

Complete step by step answer:
Mass, m= 2 kg
Velocity, v= 4 m/s towards north
Force, F= 4 N towards the west
Representing this

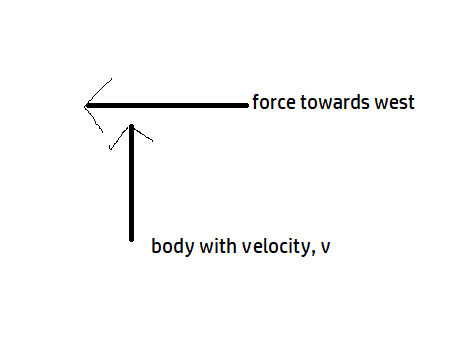
The velocity vector and the force vector both are perpendicular to each other, so the angle between them is \[90{{}^{0}}\]
Force acts on the body for 2 s
Displacement due north will be s= \[4\times 2=8m\]
Say this as \[{{s}_{1}}=8m\]----------(1)

Using second law, \[\overrightarrow{F}=m\overrightarrow{a}\]
\[4=2\overrightarrow{a}\]
\[\overrightarrow{a}=2m{{s}^{-2}}\] and this is towards the west. Now to find displacement due to the west we have to use the equation of motion.
\[s=ut+\dfrac{a{{t}^{2}}}{2}\]
Here u is the velocity towards the west but the body was moving towards north, so, u=0
\[s=\dfrac{2\times {{2}^{2}}}{2}=4m\]
So the displacement due west is 4 m in two seconds
Say this as \[{{s}_{2}}=8m\]-------(2)
From eq (1) and (2) both are vectors and both are perpendicular to each other. We have to use the parallelogram law of vector addition to add two vectors.
\[\begin{align}
  & {{s}_{net}}=\sqrt{s_{1}^{2}+s_{2}^{2}} \\
 & =\sqrt{{{4}^{2}}+{{8}^{2}}} \\
 & =\sqrt{16+64} \\
 & =\sqrt{80} \\
 & =4\sqrt{5}m \\
\end{align}\]
Hence, the net displacement of the body is \[4\sqrt{5}m\]
So, the correct option is (A)

Note: Because displacement is a vector quantity we can add it algebraically. For vectors, we have to consider their directions. Here the vectors were perpendicular so the cosine component vanishes.