Question

A body of mass 2 kg collides with a wall with a speed 100 $m{s^{ - 1}}$ are rebounds with the same speed. If the time of contact is 1/50 s, the force exerted on the wall is
A. 8 N
B. $2 \times {10^4}$ N
C. 4 N
D. ${10^4}$ N

Answer 1

THint: Before attempting this question one should have prior knowledge about the concept of momentum and also remember to use the final velocity i.e. v = - 100 m/s, use the given information to approach towards the solution.

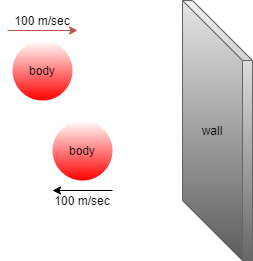
According to the given information have a body with mass 2 kg which collides on a wall with a speed of 100 $m{s^{ - 1}}$ and rebounded after 1/50 sec with the same speed as before i.e. 100 $m{s^{ - 1}}$
So the given values are initial velocity i.e. u = 100 $m{s^{ - 1}}$
Since the body will rebound in the opposite direction with the same speed therefore final velocity of the body will be – 100 $m{s^{ - 1}}$ i.e. v = - 100 $m{s^{ - 1}}$
So the change in momentum is equal to final momentum – initial momentum i.e. $\Delta p = mv - mu$
Substituting the given values in the above equation we get
$\Delta p = 2\left( { - 100 - 100} \right)$
$ \Rightarrow \Delta p = 2 \times \left( { - 200} \right)$
$ \Rightarrow \Delta p = - 400$kg m/s
So the change in momentum $|\Delta p|$ = 400 kg m/s
Since time of contact is equal to $\Delta t = \dfrac{1}{{50}}$ s
We know that the force exerted on the wall is given by \[F = \dfrac{{\Delta p}}{{\Delta t}}\]
$ \Rightarrow $ F = $\dfrac{{400}}{{\left( {1/50} \right)}}$ = $2 \times {10^4}$ N
So the force exerted on wall by body is $2 \times {10^4}$ N
Hence option B is the correct option.

Note: In the above solution we used the concept of conservation of momentum to find the force exerted on wall the concept of conversion of momentum according to which when two bodies of collide having some initial velocities in an isolated system thus the total momentum of system remain constant i.e. total momentum before collision is equal to the total momentum after collision which can be given by the equation ${m_1}{v_1} + {m_1}{v_1} = {m_1}{v_2} + {m_2}{v_1}$ here m1 and m2 are the masses of the objects colliding and v1 and v2 are the velocities of the colliding objects.