Question

A body is thrown vertically upward with a velocity ‘u’. The distance travelled by it in the 7th and 8th seconds are equal. The displacement in the 8th second is equal to? (Take g = 10 ${{\text{m}}}/{{{{\text{s}}^2}}}$)
$
  {\text{A}}{\text{. 5m}} \\
  {\text{B}}{\text{. 10m}} \\
  {\text{C}}{\text{. 2}}{\text{.5m}} \\
  {\text{D}}{\text{. }}\dfrac{5}{3}{\text{m}} \\
$

Answer 1

Hint: To find the displacement, we figure out at what point the distance travelled by the body thrown upwards can be equal in two different times. Then we apply the displacement formula to calculate the displacement in the 8th second.

Complete Step-by-Step solution:
To find, displacement in 8th second
Formula used: ${\text{s = ut + }}\dfrac{1}{2}{\text{a}}{{\text{t}}^2}$, where ‘s’ is the displacement of the object with initial velocity ‘u’ and an acceleration of ‘a’ in the time duration ‘t’.

When a body is thrown vertically upwards with some velocity, the distance travelled in its 7th and 8th seconds of travel can only become equal only if it reaches its maximum height at the end of its 7th second of travel and freely falls in its 8th second. As shown in the figure:

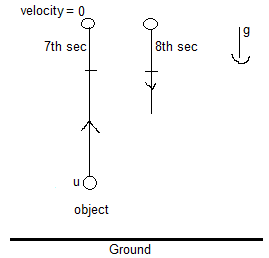
When the body reaches its maximum height, its velocity at that point of time becomes zero. As we see from the figure the velocity of the object at the end of the 7th second becomes zero. The body starts with an initial velocity equal to zero at the beginning of the 8th second and falls freely towards the ground due to the gravitational pull.
We have to compute the distance travelled by the body from the time interval 7th second till the 8th second, time duration t = 8 – 7 = 1 second.
Now we know, the displacement of a body in a time interval is given by ${\text{s = ut + }}\dfrac{1}{2}{\text{a}}{{\text{t}}^2}$
Here u = 0${{\text{m}}}/{{\text{s}}}$, t = 1sec and a = g = 10 ${{\text{m}}}/{{{{\text{s}}^2}}}$.
Hence displacement of the body in the 8th second, ${\text{s = 0 + }}\dfrac{1}{2}{\text{g}}{\left( 1 \right)^2}$
$
   \Rightarrow {\text{s = }}\dfrac{1}{2}.10.{\left( 1 \right)^2} \\
   \Rightarrow {\text{s = 5m}} \\
$
Hence displacement of the body in the 8th second is 5m.
Option A is the correct answer.

Note – In order to answer this type of questions the key is to know the phenomena of a body thrown vertically upwards under the influence of gravity, its trajectory and its properties. Having knowledge in this concept helps us directly relate to when a body can have equal displacement at two different time intervals.
While a body is thrown upwards with an initial velocity, it keeps gaining its potential energy and losing its kinetic energy as it goes upwards and vice versa when it falls downwards but the total energy of the body is conserved at all times.