Question

A body is thrown up with a finite speed and is caught back after $4s$. The speed with which the body is thrown up is
A. $10m/s$
B. $20m/s$
C. $30m/s$
D. $40m/s$

Answer 1

Hint: At the moment the particle is on the ground, its displacement is zero but it has an initial velocity with which it will be thrown upwards. With these boundary conditions we can determine the initial velocity by substituting them in the displacement equation, second equation in the equations that govern motion in two dimensions.


Formulae used:
Displacement equation: $S = ut + \dfrac{1}{2}a{t^2}$
Where $S$ is the displacement of the body and is expressed in meters $(m)$, $u$ is the initial velocity of the particle and is expressed in meters per second $(m/s)$, $a$ is the acceleration acting on the body and is expressed in meter per second square $(m/{s^2})$ and $t$ is the time period of motion of the body and is expressed in seconds $(W)$.

Complete step by step answer:
The body is thrown up and returns back to the same position after $4s$. This means that the body has not displaced, that is $S = 0$.

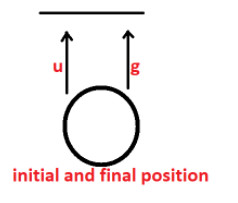
It is thrown with some speed and this is denoted by $u$. While going up, this speed pushes it but the acceleration due to gravity is pulling it down, trying to inhibit its motion. That is, $a = - g$.
 While coming down, the acceleration due to gravity pulls it downwards. The body completes the motion in $4s$.
The moment it returns, it has no velocity. It is in a state of rest.
Using these conditions, we can find out $u$.
We know that, $S = ut + \dfrac{1}{2}a{t^2}$ .
Substituting the given data and boundary conditions, we get,
$
  S = ut + \dfrac{1}{2}a{t^2} \\
   \Rightarrow 0 = u(4) + \dfrac{1}{2}( - g){(4)^2} \\
   \Rightarrow 0 = u(4) + \dfrac{1}{2}( - 10){(4)^2} \\
   \Rightarrow u = 40m/s \\
 $
Thus, the speed with which the body is thrown up is $40m/s$.
In conclusion, the correct option is D.

Note:This problem can only be solved when we evaluate it at the moment it returns back. Displacement will be zero and we also know the entire time period of motion. Also, acceleration due to gravity inhibits the motion of the body while going upwards but, it is the only acceleration acting on the body.