Question

A body is suspended by a string from the ceiling of an elevator. It is observed that the tension in the string is doubled when the elevator is accelerated. The acceleration will be?
A. ${\text{ a = 4}}{\text{.9 m/}}{{\text{s}}^2}$
B. ${\text{ a = 9}}{\text{.8 m/}}{{\text{s}}^2}$
C. ${\text{ a = 19}}{\text{.6 m/}}{{\text{s}}^2}$
D. ${\text{ a = 2}}{\text{.45 m/}}{{\text{s}}^2}$

Answer 1

Hint: In order to solve this question, we would require Newton's second law of motion along with we have to take pseudo force into action so as to solve the question in a fast and easy way. As pseudo force makes the question simple. Gravitational force and tension would also be used to solve the question

Formula used:
$force = mass \times acceleration$ or we could say , $F = ma$

Complete step by step answer:
To understand this question clearly we need to use the diagram before the acceleration is applied and after the acceleration is applied. Before acceleration is applied, the body is suspended by a string from the ceiling of an elevator.

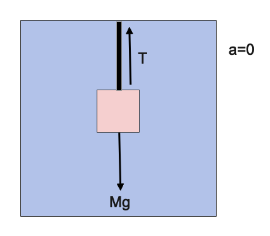
$T$: tension applied by the string pushing the body upward.
$Mg$: gravity acting on the body and creating a downward force.
$g$: gravitational constant is $9.8$.
$a=0$ denotes that the elevator is at rest no acceleration is applied.
Here as acceleration is zero
$T = Mg$…. (Equation 1)
After acceleration is applied, the body is suspended by a string from the ceiling of an elevator.

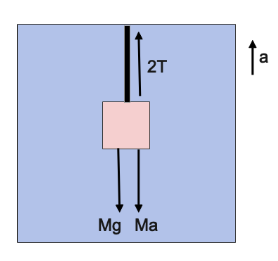
This diagram is the scenario what question says
$2T$: twice the tension is pulling the box upward.
$Mg$: it acts the same as in the above scenario.
$Ma$: force because of the second law of newton.

$Ma$ is pulling the box downward while the elevator is accelerated upward. This is because when we see the scenario from inside the elevator the applying the pseudo for the force will be applied in the opposite direction. This is all because of the frame of reference of seeing a body from inside or outside. Here both the mg and ma acting downward while twice the tension is applied upward
$2T = Ma + Mg$ …. (Equation 2)
Putting Equation 1 in Equation 2
$2Mg = Ma + Mg$
$\Rightarrow 2Mg - Mg = Ma$
$\Rightarrow Mg = Ma$
Both the mass will be cut down and the acceleration would be:
$\therefore a = g$

Therefore, option B is the correct answer.

Note: Newton’s second law of motion can only be applied when acceleration is constant if it is not constant then none of the Newton law can be applied. Stretching of the string tightly causes the tension force on the body to solve this kind of question frame of reference should be right.