Question

A body is moving with velocity $30m{{s}^{-1}}$ towards east. After $10s$, its velocity becomes $40m{{s}^{-1}}$ towards the north. The average acceleration of the body is
$\begin{align}
  & A)5m{{s}^{-2}} \\
 & B)1m{{s}^{-2}} \\
 & C)7m{{s}^{-2}} \\
\end{align}$
$D)$none of these

Answer 1

Hint: The velocity towards east is taken as a vector moving in the positive $x$ direction. Similarly, the velocity towards north is taken as a vector moving in the positive $y$ direction. Magnitude of change in both these vectors is determined. Acceleration is equal to the ratio of change in velocity to the change in time.

Formula used:
${{a}_{avg}}=\dfrac{\Delta v}{dt}$

Complete step by step answer:
We are told that a body is moving towards the east with an initial velocity of $30m{{s}^{-1}}$. After $10s$, the same body moves to the north direction with a final velocity of $40m{{s}^{-1}}$.

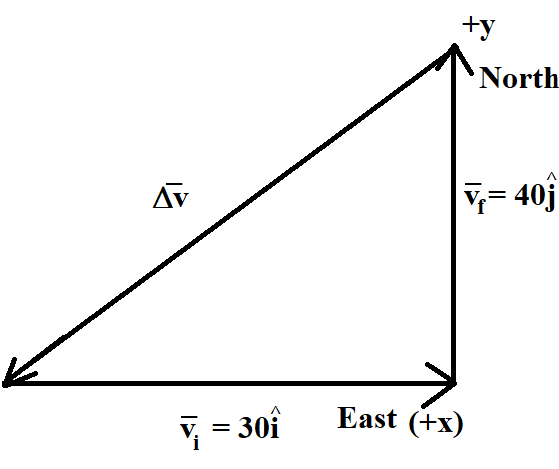
If we consider the initial velocity of the body to be moving along a unit vector $i$ in the positive $x$ direction, the initial velocity can be written as
$\overrightarrow{{{v}_{i}}}=30\widehat{i}$
where
$\overrightarrow{{{v}_{i}}}$ is the initial velocity of the body moving towards east
$30$ is the magnitude of initial velocity of the body
$\overrightarrow{i}$ is the unit vector along the positive $x$ direction
Let this be equation 1.
Similarly, if we consider the final velocity of the body to be moving along a unit vector $\widehat{j}$ in the positive $y$ direction, the final velocity can be written as
$\overrightarrow{{{v}_{f}}}=40\widehat{j}$
where
$\overrightarrow{{{v}_{f}}}$ is the final velocity of the body moving towards north
$40$ is the magnitude of final velocity of the body
$\widehat{j}$ is the unit vector along the positive $y$ direction
Let this be equation 2.
Now, change in velocity of the body is given by
$\overrightarrow{\Delta v}=\overrightarrow{{{v}_{f}}}-\overrightarrow{{{v}_{i}}}=40\widehat{j}-30\widehat{i}$
The magnitude of change in velocity is given by
$\Delta v=\left| \sqrt{{{40}^{2}}+{{30}^{2}}} \right|=50m{{s}^{-1}}$
where
$\Delta v$ is the magnitude of change in velocity of the body
$30$ is the magnitude of initial velocity
$40$ is the magnitude of final velocity
Let this be equation 3.
Now, we know that the average acceleration of a body is the ratio of change in velocity of the body to the change in time. Therefore, if the average acceleration of the given body is denoted as ${{a}_{avg}}$, it is given by
${{a}_{avg}}=\dfrac{\Delta v}{dt}$
where
${{a}_{avg}}$ is the average acceleration of a body
$\Delta v$ is the change in velocity of the body
$dt$ is the change in time
Let this be equation 4.
Here, we are given that time required for the body to change from its initial value of velocity to the final value of the velocity is $10s$. Clearly,
$dt=10s$
Let this be equation 5.
Substituting equation 5 and equation 3 in equation 4, we have,
${{a}_{avg}}=\dfrac{\Delta v}{dt}=\dfrac{50m{{s}^{-1}}}{10s}=5m{{s}^{-2}}$
Therefore, the average acceleration of the given body is equal to $5m{{s}^{-2}}$. The correct answer is option $A$.

Note:
Students need to understand that only the magnitude of acceleration is asked here. Therefore, it is enough for us to calculate the magnitude of change in velocity with respect to time. Clearly, in equation 3, we have considered the magnitude of change in velocity vector as $\left| \overrightarrow{\Delta v} \right|=\Delta v$. If direction was considered, we would have ended up with the average acceleration of the body in the north-east direction. Students can easily arrive at this direction with the help of vector analysis.