Question

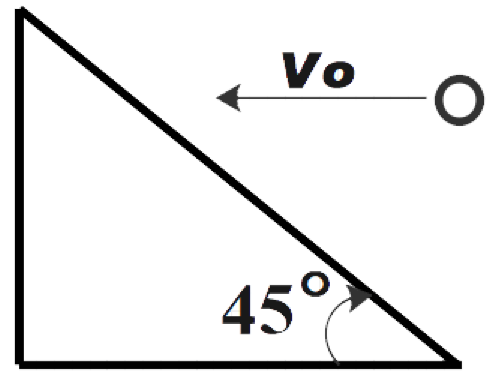
A body is made in the form of a wedge with an angle 45. See figure. A ball of mass m, moving horizontally with the speed \[{{V}_{o}}=\sqrt{2}\] collides with the wedge of mass 2m. As a result of impact, the ball bounces vertically upward. Neglect the friction between wedge and horizontal surface. The speed of the ball just after the impact is:
                  

A. 0.5 m/s
B. 2 m/s
C. \[\sqrt{2}\] m/s
D. 1 m/s

Answer 1

Hint: In this question we have been asked to calculate the velocity of the ball after the collision with the wedge. To solve this question, we shall be using the conservation of momentum in horizontal direction. By using this method, we shall calculate the velocity of the wedge as the velocity of the ball is given. Later, we shall use the conservation of energy method, to calculate the velocity of the ball just after impact.

Complete answer:
Let us assume that the speed of the ball just after the impact is V and that of the wedge is \[{{V}_{1}}\].
Now, after the collision the horizontal component of velocity of the ball is zero as shown in the figure.
Therefore, applying the conservation of momentum for ball and wedge, after the collision in horizontal can be given by,
\[m{{v}_{o}}+0=2m\times {{V}_{1}}\]
After substituting given values
We get,
\[\sqrt{2}=2{{V}_{1}}\]
Therefore,
\[{{V}_{1}}=\dfrac{1}{\sqrt{2}}m/s\] …………… (1)
Now, applying the energy conservation for the same system
We get,
\[\dfrac{1}{2}mV_{o}^{2}=\dfrac{1}{2}(2m)V_{1}^{2}+\dfrac{1}{2}m{{V}^{2}}\]
After substituting the values
We get,
\[{{(\sqrt{2})}^{2}}=2V_{1}^{2}+{{V}^{2}}\]
Substituting from (1)
 We get,
\[2=2\times \dfrac{1}{2}+{{V}^{2}}\]
Therefore,
\[V=1m/s\]

Therefore, the correct answer is option D.

Note:
The law of conservation of energy states that the energy can neither be created nor can it be destroyed. However, it can be transferred from one type to another. This law helps in finding information about the object such as its height, velocity and mass. The law of conservation of momentum as given by Newtons, states that the momentum of an isolated system remains constant.