Question

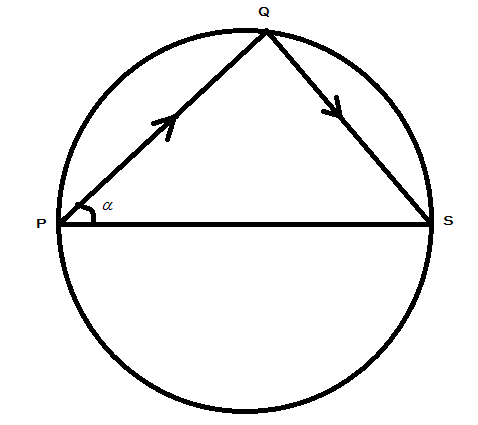
A body is fired from pt. P and strikes at Q inside a smooth circular wall as shown in figure. It bounds to pt. S (diametrically opposite to P). The coefficient of restitution will be:
(A) $ \cot \alpha $
(B) $ 1 $
(C) $ \tan \alpha $
(D) $ {\tan ^2}\alpha $

Answer 1

Hint :We have given the diagram that a body is fired up from P, hits at Q and bounds at point S and this point S is opposite of point Q. We have to use simple geometry concepts here like drawing normal from point Q and thus draw the components acting on the body at point Q.

Complete Step By Step Answer:
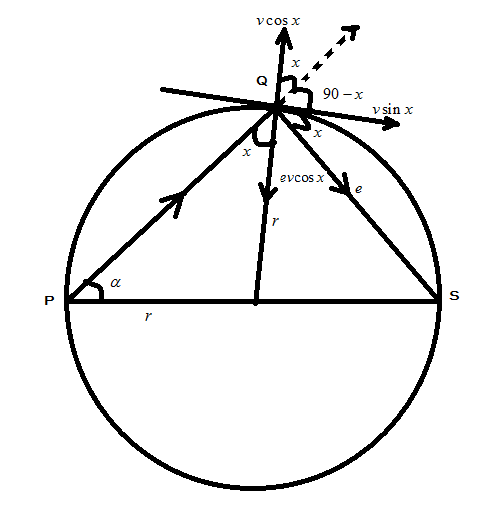
Let us draw the components first in the given diagram by naming them as shown in the figure below: let us now explain the components given in the figure
A normal is drawn through Q such that it crosses the center of the circle and makes a angle called $ x $ with radii and line joining P and Q. a horizontal component is named as $ v\sin x $ where $ v $ is the velocity of the body that is fired from the point P, the vertical component is named as $ v\cos x $ . Now, the line joining Q and S is called as the direction of restitution and we named it as $ e $ and the component of restitution along the radius towards the center is $ ev\cos x $ .
Now, we want to find out the coefficient of restitution $ e $ :
Therefore, $ \tan x = \dfrac{{ev\cos x}}{{v\sin x}} $
 $ \Rightarrow \tan x = \dfrac{e}{{\tan x}} $
 $ \Rightarrow e = {\tan ^2}x $
But the angle subtended by a diameter is right angled triangle (properties of circle)
Now, the triangle formed by $ r $ , $ r $ and PQ is an isosceles triangle such that angles
 $ x = \alpha $

Thus as we have
 $ \Rightarrow e = {\tan ^2}x $
Can be written as
 $ \Rightarrow e = {\tan ^2}\alpha $
Therefore, the restitution coefficient is given by $ e = {\tan ^2}\alpha $ .
The correct answer is option D.

Note :
We have been given the smooth circular surface therefore we haven’t resolved the component of friction caused by the body hitting at point Q. The coefficient of restitution is the ratio between initial velocity and final velocity of the body.