Question

A body is falling freely from a point A at a certain height from the ground and passes through points \[B,C\;and\;D\;\] (vertically as shown) so that \[BC = CD\] . The time taken by the particle to move from \[B\;to\;C\;\] is \[2\;seconds\] and from \[C\;to\;D\;\] is \[1{\text{ }}second\] . Time taken to move from \[A\;to\;B\;\] in seconds is

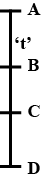
(a) 0.6
(b) 0.5
(c) 0.4
(d) 0.2

Answer 1

Hint: Using the formula of the law of motion equations, this problem is often solved. This problem solution is mainly based on the formation of the equations of distances and then finding the difference between the identical.

Formula used: \[v = u + gt\]
\[S = ut + \dfrac{1}{2}g{t^2}\]
Where, \[u\]-initial velocity, \[v\]-final velocity, \[t\]-time taken and \[S\]-distance traveled

Complete step-by-step solution:
The velocity of the body at point A, \[{u_A} = 0\]
Let the velocity of the body at point B and C will be \[{u_B},{u_C}\]
Let \[BC = CD = S\]
For journey A to B\[ \Rightarrow {u_B} = {u_A} + g{t_{AB}}\]
Where \[{t_{AB}}\] is the time taken to move from A to B
\[{u_B} = 10{t_{AB}}\]
\[\left( {\therefore {u_A} = 0} \right)\]\[ - - - - - - \left( 1 \right)\]
For journey B to C\[ \Rightarrow {u_C} = {u_B} + g{t_{BC}}\]
\[{u_C} = {u_B} + 20\] \
[\left( {\therefore {t_{BC}} = 2} \right)\]
We get \[S = {u_B}{t_{BC}} + \dfrac{1}{2}gt_{BC}^2\]
\[S = 2{u_B} + 20\]\[ - - - - - - \left( 2 \right)\]
For journey C to D\[ \Rightarrow {u_D} = {u_C} + g{t_{CD}}\]
\[{u_D} = {u_C} + 10\]
\[\left( {\therefore {t_{BC}} = 1} \right)\]
We get \[S = {u_C}{t_{CD}} + \dfrac{1}{2}gt_{CD}^2\]
\[S = {u_C} + 5\]\[ - - - - - - \left( 3 \right)\]
Equation (2)-(3), we get
$\Rightarrow$\[S - S = 2{u_B} + 20 - {u_C} - 5\]
$\Rightarrow$\[0 = 2{u_B} - {u_C} + 15\]
\[\left( {\therefore {u_C} = {u_B} + 20} \right)\]
$\Rightarrow$\[0 = 2{u_B} - {u_B} - 20 + 15\]
$\Rightarrow$\[{u_B} = 5\]
From equation 1, we get
$\Rightarrow$\[{u_B} = 10{t_{AB}}\]
$\Rightarrow$\[5 = 10{t_{AB}}\]
$\Rightarrow$\[{t_{AB}} = \dfrac{1}{2} = 0.5s\]
Hence, the time taken to move from A to B is \[0.5\sec \].
Option (b) is the correct answer.

Note: A particle is freely falling under the influence of gravity, so, we’ll make use of the law of motion formulae to resolve this problem.
The equation of the second law of motion is given as follows:
\[S = ut + \dfrac{1}{2}a{t^2}\] Where, \[s\]is the distance, \[u\]is initial velocity, \[t\] is the time, and \[a\] is the acceleration.
This equation of the second law of motion should be expressed in terms of height reached by the particle and also the acceleration should be replaced with gravitational constant.
Thus, we get,
\[h = ut + \dfrac{1}{2}g{t^2}\]