Question

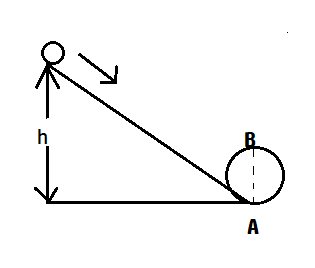
A body initially at rest and sliding along a frictionless track from a height h (as shown in the figure) just completes a vertical circle of diameter AB = D. the height h is equal to?

1- \[\dfrac{3D}{2}\]
2- D
3- \[\dfrac{7D}{5}\]
4- \[\dfrac{5D}{4}\]

Answer 1

Hint: The body moves down the track and the track is frictionless, so there is a question of friction force coming into play. Also, it is given that the body completes a vertical circle so we can use the energy conservation at the top and the bottom to arrive at a meaningful solution.

Complete step by step answer:
Energy at the top= Energy at the bottom
At top there is only potential energy and at the bottom the energy is completely kinetic, so,
\[mgh=\dfrac{m{{v}^{2}}}{2}\]
\[h=\dfrac{{{v}^{2}}}{2g}\]-----(1)
For completing the vertical circle, the velocity at the lowest point must satisfy the condition, \[v\ge \sqrt{5gr}\] where r is the radius and equal to half of diameter.
So, eq (1) becomes,
$
h=\dfrac{5gr}{2g} \\
\implies h=\dfrac{5}{2}r \\
\therefore h=\dfrac{5}{4}D \\
$

So, the correct answer is “Option 4”.

Additional Information:
Motion in a vertical circle is not uniform circular motion. Also the law of conservation of energy holds until and unless no external force acts on the system and there is no loss of energy in the form of heat and light.

Note:
while doing such problems we should be careful to see whether the body completes the vertical circle or not. Also, if the track is not frictionless, there will come friction force and we have to take that into account too. The weight of the body always acts downwards.