
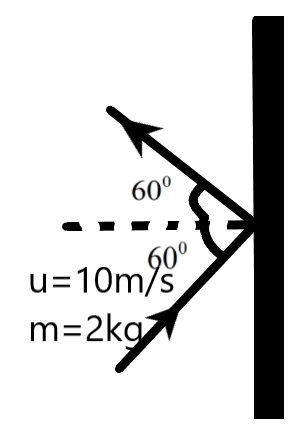
A body hits the wall as in the figure if collision is perfectly elastic, then find the impulse imparted in the wall (collision is perfectly elastic).

Answer
559.8k+ views
Hint: We need to understand the relation between the impulse imparted on an object due to collision with the mass and velocity of the colliding body. We can introduce the law of conservation of linear momentum to find this relation more easily.
Complete step-by-step answer:
The impulse imparted on a body is defined as the force experienced by a body under collision for the time interval of collision. It is given as –
\[\text{Impulse, }I=F.\Delta t\]
We know that the impulse imparted can also be related to the linear momenta of the object before and after collision. The impulse imparted on the object which was collided by another object is defined as the change in linear momentum of the body which collides before and after collision.
\[I={{m}_{1}}{{v}_{1}}-{{m}_{2}}{{v}_{2}}\]
We know that according to the conservation of linear momentum, in a perfectly elastic collision, the magnitude of the momentum before and after collision remains the same. But, the direction of the momentum changes.
Let us consider the situation given to us.
A ball is hitting a wall on which a certain impulse is imparted. We know that the angle of incidence of the ball and the angle of rebounding will be equal in a perfectly elastic collision. We can find the velocity along the x-axis using the cosine function.
\[\begin{align}
& \text{given,} \\
& \theta ={{60}^{0}} \\
& {{v}_{1}}=u\cos \theta \\
& \Rightarrow {{v}_{1}}=10\cos ({{60}^{0}}) \\
& \therefore {{v}_{1}}=5m{{s}^{-1}} \\
& \text{similarly,} \\
& {{v}_{2}}=u\cos \theta \\
& \Rightarrow {{v}_{2}}=10\cos ({{60}^{0}}) \\
& \therefore {{v}_{2}}=5m{{s}^{-1}} \\
\end{align}\]
Now, we can find the impulse imparted on the wall by the ball. The direction of velocity along the x-axis is in the opposite direction for incidence and the rebound condition.
i.e.,
\[\begin{align}
& I={{m}_{1}}{{v}_{1}}-{{m}_{2}}{{v}_{2}} \\
& \Rightarrow I=2kg(5m{{s}^{-1}})\widehat{i}-2kg(-5m{{s}^{-1}})\widehat{i} \\
& \therefore I=+20\widehat{i}kgm{{s}^{-1}} \\
\end{align}\]
The impulse imparted on the wall is along the positive x-axis with a magnitude of 20\[kgm{{s}^{-1}}\].
This is the required solution.
Note: The impulse imparted on the wall during the time of collision is the reason for the change in direction of the colliding ball. The magnitude of the momentum before and after collision can be conserved, but the direction change is contributed by the impulse.
Complete step-by-step answer:
The impulse imparted on a body is defined as the force experienced by a body under collision for the time interval of collision. It is given as –
\[\text{Impulse, }I=F.\Delta t\]
We know that the impulse imparted can also be related to the linear momenta of the object before and after collision. The impulse imparted on the object which was collided by another object is defined as the change in linear momentum of the body which collides before and after collision.
\[I={{m}_{1}}{{v}_{1}}-{{m}_{2}}{{v}_{2}}\]
We know that according to the conservation of linear momentum, in a perfectly elastic collision, the magnitude of the momentum before and after collision remains the same. But, the direction of the momentum changes.
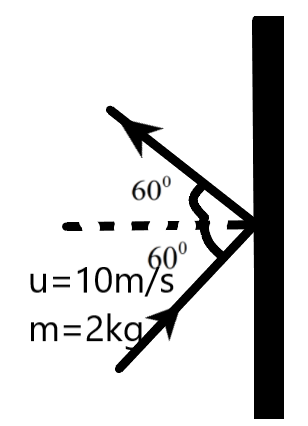
Let us consider the situation given to us.

A ball is hitting a wall on which a certain impulse is imparted. We know that the angle of incidence of the ball and the angle of rebounding will be equal in a perfectly elastic collision. We can find the velocity along the x-axis using the cosine function.
\[\begin{align}
& \text{given,} \\
& \theta ={{60}^{0}} \\
& {{v}_{1}}=u\cos \theta \\
& \Rightarrow {{v}_{1}}=10\cos ({{60}^{0}}) \\
& \therefore {{v}_{1}}=5m{{s}^{-1}} \\
& \text{similarly,} \\
& {{v}_{2}}=u\cos \theta \\
& \Rightarrow {{v}_{2}}=10\cos ({{60}^{0}}) \\
& \therefore {{v}_{2}}=5m{{s}^{-1}} \\
\end{align}\]
Now, we can find the impulse imparted on the wall by the ball. The direction of velocity along the x-axis is in the opposite direction for incidence and the rebound condition.
i.e.,
\[\begin{align}
& I={{m}_{1}}{{v}_{1}}-{{m}_{2}}{{v}_{2}} \\
& \Rightarrow I=2kg(5m{{s}^{-1}})\widehat{i}-2kg(-5m{{s}^{-1}})\widehat{i} \\
& \therefore I=+20\widehat{i}kgm{{s}^{-1}} \\
\end{align}\]
The impulse imparted on the wall is along the positive x-axis with a magnitude of 20\[kgm{{s}^{-1}}\].
This is the required solution.
Note: The impulse imparted on the wall during the time of collision is the reason for the change in direction of the colliding ball. The magnitude of the momentum before and after collision can be conserved, but the direction change is contributed by the impulse.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




