Question

A body dropped from a height $h$ with initial velocity zero, strikes the ground with a velocity $3m{{s}^{-1}}$. Another body of the same mass dropped from the same height $h$ with an initial velocity of $4m{{s}^{-1}}$. The final velocity of second mass, with which it strikes the ground, is
$\begin{align}
  & \text{A}\text{. }5m{{s}^{-1}} \\
 & \text{B}\text{. }12m{{s}^{-1}} \\
 & \text{C}\text{. }3m{{s}^{-1}} \\
 & \text{D}\text{. }4m{{s}^{-1}} \\
\end{align}$

Answer 1

Hint: A free falling object is an object that is falling under the sole influence of gravitational force. An object dropped from some height is considered as in a state of free fall. For the object in free fall, we can apply the Kinematic equations with acceleration of the object equal to the acceleration due to gravity. By applying the equation of uniformly accelerated motion on the first body’s motion, will calculate the height through which the bodies are dropped and applying the equation on the second body, by putting the same value of height, will give the final velocity with which the second body strikes the ground.

Formula used:
Equation of uniformly accelerated motion,
${{v}^{2}}-{{u}^{2}}=2as$

Complete step-by-step answer:
When an object is dropped from some height, the motion of the object is considered as free fall. In this case, the air resistance acting on the object is considered as negligible. The force of gravity causes the object to fall towards the center of the Earth. The acceleration of the free falling object is therefore called the acceleration due to gravity. The acceleration due to gravity is a universal constant, which means we can apply the kinematics equations to any freely falling object where air resistance and friction on the object are negligible. 
If gravity is the only influence acting on the object, then the acceleration is always in the downward direction. The acceleration due to gravity has the same magnitude for all bodies, and is denoted by the symbol $g$.
Kinematic equations for the object in free-fall where the acceleration due to gravity is considered as $-g$
$\begin{align}
  & v=u-gt \\
 & s=ut-\dfrac{1}{2}g{{t}^{2}} \\
 & {{v}^{2}}={{u}^{2}}-2gs \\
\end{align}$
Where,
$u$ is the initial speed of the body
$v$ is the final speed of the body
$s$ is the displacement of the object
$g$ is the acceleration due to gravity
$t$ is the time taken by the object
We are given that a body dropped from a height $h$ with initial velocity zero, strikes the ground with a velocity $3m{{s}^{-1}}$ and the another body of same mass dropped from the same height $h$ is dropped with an initial velocity of $4m{{s}^{-1}}$. We have to calculate the final velocity of the second mass, with which it strikes the ground.

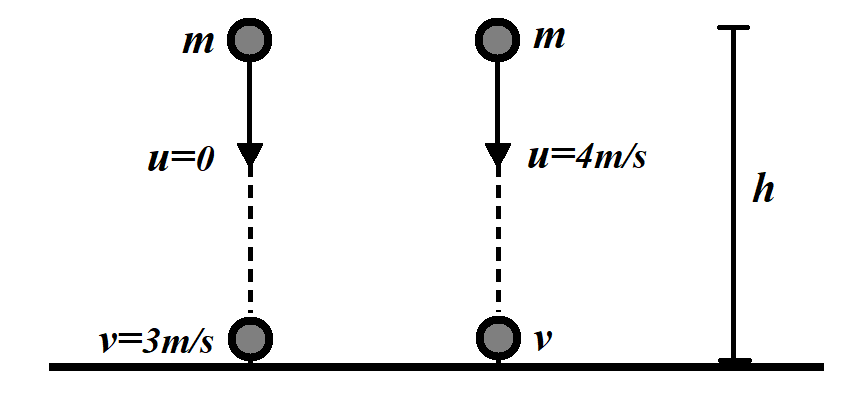
Initial speed of first body, ${{u}_{1}}=0$
Final speed of first body, ${{v}_{1}}=3m{{s}^{-1}}$
Initial speed of second body, ${{u}_{2}}=4m{{s}^{-1}}$
Final speed of second body, let’s say ${{v}_{2}}$
As we know, the body is dropped with height $h$
As we know, the body is in free fall, which means that the acceleration of the body is equal to the acceleration due to gravity.
$a=g$
Applying the equation of motion for first body,
${{v}^{2}}-{{u}^{2}}=2as$
Putting,
$\begin{align}
  & v=3m{{s}^{-1}} \\
 & u=0 \\
 & a=g \\
 & s=h \\
\end{align}$
We get,
$\begin{align}
  & {{\left( 3 \right)}^{2}}-0=2gh \\
 & 9=20h \\
 & h=\dfrac{9}{20}m \\
\end{align}$
As the second object is dropped from the same height,
Applying the equation of motion for second body,
${{v}^{2}}-{{u}^{2}}=2as$
Putting,
$\begin{align}
  & u=4m{{s}^{-1}} \\
 & a=g \\
 & s=\dfrac{9}{20}m \\
\end{align}$
We get,
$\begin{align}
  & {{v}^{2}}-{{\left( 4 \right)}^{2}}=2\times 10\times \dfrac{9}{20} \\
 & {{v}^{2}}=16+9=25 \\
 & v=5m{{s}^{-1}} \\
\end{align}$
The final velocity of second mass, with which it strikes the ground, is $5m{{s}^{-1}}$

So, the correct answer is “Option A”.

Note: Free fall is any motion of an object where gravity, or gravitational force, is the only force acting upon it. In the context of general relativity, where gravitation is reduced to a space-time curvature, an object in free fall has no force acting on it.
An object in the free fall may not necessarily be falling down to the ground in the usual sense of the term. An object moving upwards would not normally be considered to be falling, but if it is subject to the force of gravity only, means that the air resistance and friction on the object are assumed to be negligible, it is said to be in free fall.