Question

A boat travels from south bank to north bank of a river with a maximum speed of $8Km{{h}^{-1}}$. A river current flows from west to east with a speed of $4Km{{h}^{-1}}$. To arrive at a point the opposite to the point of start, boat should start with an angle:
$\begin{align}
  & \text{A}\text{. ta}{{\text{n}}^{-1}}\left( \dfrac{1}{2} \right)\text{W of N} \\
 & \text{B}\text{. ta}{{\text{n}}^{-1}}\left( \dfrac{1}{2} \right)\text{N of W} \\
 & \text{C}\text{. 3}{{0}^{\circ }}\text{W of N} \\
 & \text{D}\text{. 3}{{0}^{\circ }}\text{N of W} \\
\end{align}$

Answer 1

Hint: The resultant velocity of the boat is the vector sum of the boat velocity and the river velocity. The boat always heads straight across the river and the river current is always directed straight downstream, therefore, the two vectors are at right angles to each other.

Complete step by step answer:
We are given that a boat travels from south bank to north bank of the river with maximum speed. We need to calculate the angle with which the boat should start to arrive at the opposite end of its start.

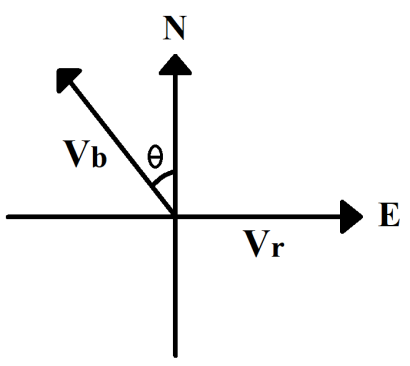
Let ${{V}_{b}}$ be the velocity of the boat, and
${{V}_{r}}$ be the velocity of the river water
Let the boat starts at an angle $\theta $
In order to reach the opposite end of the starting point, the horizontal component of the boat’s velocity should be equal to the velocity of the river in the same direction.
Now,
${{V}_{b}}\sin \theta ={{V}_{r}}$
Given that,
$\begin{align}
  & {{V}_{b}}=8Km{{h}^{-1}} \\
 & {{V}_{r}}=4Km{{h}^{-1}} \\
\end{align}$
$\sin \theta =\dfrac{{{V}_{r}}}{{{V}_{b}}}$
Therefore,
$\begin{align}
  & \sin \theta =\dfrac{4}{8}=\dfrac{1}{2} \\
 & \theta ={{30}^{\circ }}\text{W of N} \\
\end{align}$
The boat should start at an angle ${{30}^{\circ }}\text{W of N}$
Hence, the correct option is C.

Note:
If a motorboat is supposed to head straight across a river, that is, if the boat were to point its bow straight towards the other side, it would not reach the shore directly across from its initial point. The river current always tries to influence the motion of the boat and carries it downstream. The motorboat may be moving with a velocity of $x\text{ }m{{s}^{-1}}$ directly across the river, yet the resultant velocity of the boat will be greater than $x\text{ }m{{s}^{-1}}$ and at an angle in the downstream direction.