Question

A boat travels 10 miles east and then 24 miles south to an island. How many miles are there from the point of departure of the boat to the boat to the island?
A. 34
B. 14
C. 26
D. $2\sqrt{119}$
E. 44

Answer 1

Hint: In such questions, ‘distance from the starting point’ refers to the shortest distance between the start point and the end point. Most of these questions involve the creation of right-angled triangles and then applying the Pythagoras theorem. It is advisable to draw a diagram and then solve such problems.

Complete step-by-step solution:

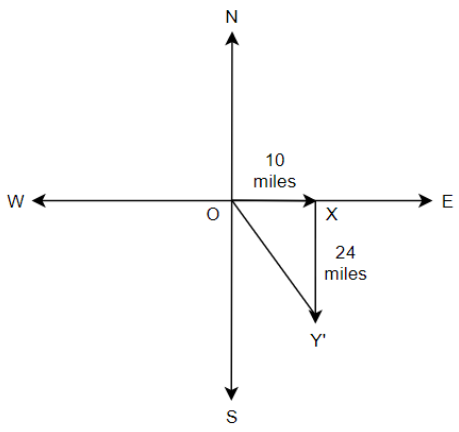
Let us assume a boat starts at a point O. First it moves east 10 miles to X and then it moves south 24 miles to Y. As can be seen from the diagram, its distance from the starting point (Meaning shortest distance) is $OY'$. Therefore finding out the length of $OY'$ will give us the answer. We know that the directions east and south are perpendicular to each other. Therefore, we can say that the triangle $OXY'$ is a right angled triangle at X.
As $OXY'$ is a right angled triangle, we can apply Pythagoras theorem here. Pythagoras theorem is:
\[\begin{align}
&\text{Bas}{{\text{e}}^{2}}+\text{perpendicula}{{\text{r}}^{2}}=\text{Hypotenus}{{\text{e}}^{2}} \\
 & \Rightarrow O{{X}^{2}}+{{\left( XY' \right)}^{2}}={{\left( OY' \right)}^{2}} \\
 & \Rightarrow {{10}^{2}}+{{24}^{2}}={{\left( OY' \right)}^{2}} \\
 & \Rightarrow 100+576={{\left( OY' \right)}^{2}} \\
 & \Rightarrow {{\left( OY' \right)}^{2}}=676 \\
 & \Rightarrow OY'=26\text{miles} \\
\end{align}\]
Hence the correct answer is C.

Note: Such questions can be solved quickly if you can remember the Pythagorean triplets. Below are a few: (3, 4, 5), (5, 12, 13), (7, 24, 25). This question uses the (5, 12, 13) triplet. Just multiply the set by 2 and you get another triplet, $\left( 5,12,13 \right)\times 2=\left( 10,24,26 \right)$.