Question

A boat is to cross a river of width $500\,m$. The velocity of the river flow is $5\,kmph$ and the velocity of the boat is $10\,kmph$. The angle at which the boat is to be rowed with the direction of river flow velocity so that the boat can cross the river along shortest path is
$\begin{align}
  & A.\,\,{{120}^{\circ }} \\
 & B.\,\,{{135}^{\circ }} \\
 & C.\,\,{{150}^{\circ }} \\
 & D.\,\,{{60}^{\circ }} \\
\end{align}$

Answer 1

Hint: The boat should row diagonally in the opposite direction of the river flow at a certain angle, such that the combination of the boat speed, river flow and the angle will give us the shortest path that the boat should take to cross the river.

Formula used:
$\sin \theta =\dfrac{Perpendicular}{Hypotenuse}$

Complete step by step answer:
The scenario depicted in the question can be represented as shown below:

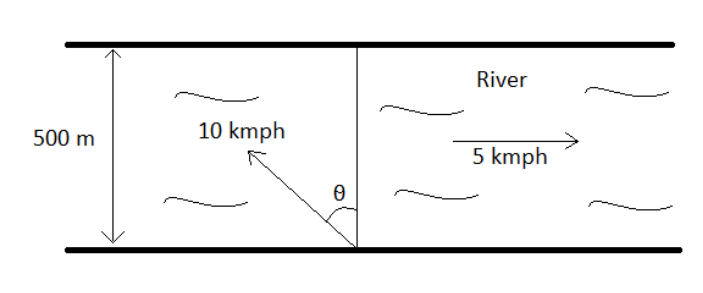
From the figure it is clear that we need to find $\theta $, such that the angle at which the boat is to be rowed with the direction of river flow velocity so that the boat can cross the river along shortest path will be $({{90}^{\circ }}+\theta )$.
Now,
From the diagram we can deduce the below figure to calculate $\theta $:

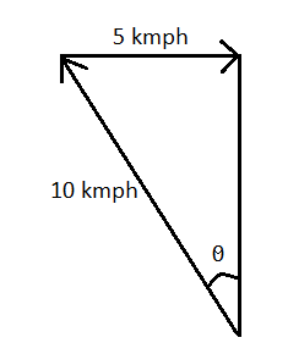
We know that,
$\sin \theta =\dfrac{Perpendicular}{Hypotenuse}$
Hence,
$\sin \theta =\dfrac{5}{10}=\dfrac{1}{2}$
$\Rightarrow \theta ={{30}^{\circ }}$
Since, we have got $\theta ={{30}^{\circ }}$, then the angle at which the boat is to be rowed with the direction of river flow velocity so that the boat can cross the river along shortest path will be $({{90}^{\circ }}+{{30}^{\circ }})$, i.e., ${{120}^{\circ }}$.
Therefore, the correct answer is Option (A).

Note:
In this type of question, the direction of the river flow is most important. If the river flow direction is not given, then we can assume any direction according to our need, but if it is explicitly mentioned, then follow that direction to solve the question.