Question

A boat covers a certain distance downstream in 1 hour, while it comes back in $1\dfrac{1}{2}hours$. If the speed of the stream be 3 kmph, what is the speed of the boat in still water?
A. 12 kmph
B. 13 kmph
C. 14 kmph
D. 15 kmph
E. None of these

Answer 1

Hint: We will be using the concepts of time distance and speed to solve the problem. We will also be using the concepts of upstream and downstream in which the speed of the boat increases when it flows with the downstream and decreases when it flows with the upstream.

Complete step-by-step answer:
Now, we have been given that the boat covers a certain distance in downstream in 1 hour, while covering the same in upstream took $1\dfrac{1}{2}hours$.
Also, we have been given that the speed of the stream is 3kmph. We will let the speed of the boat in still water as x km/hr.

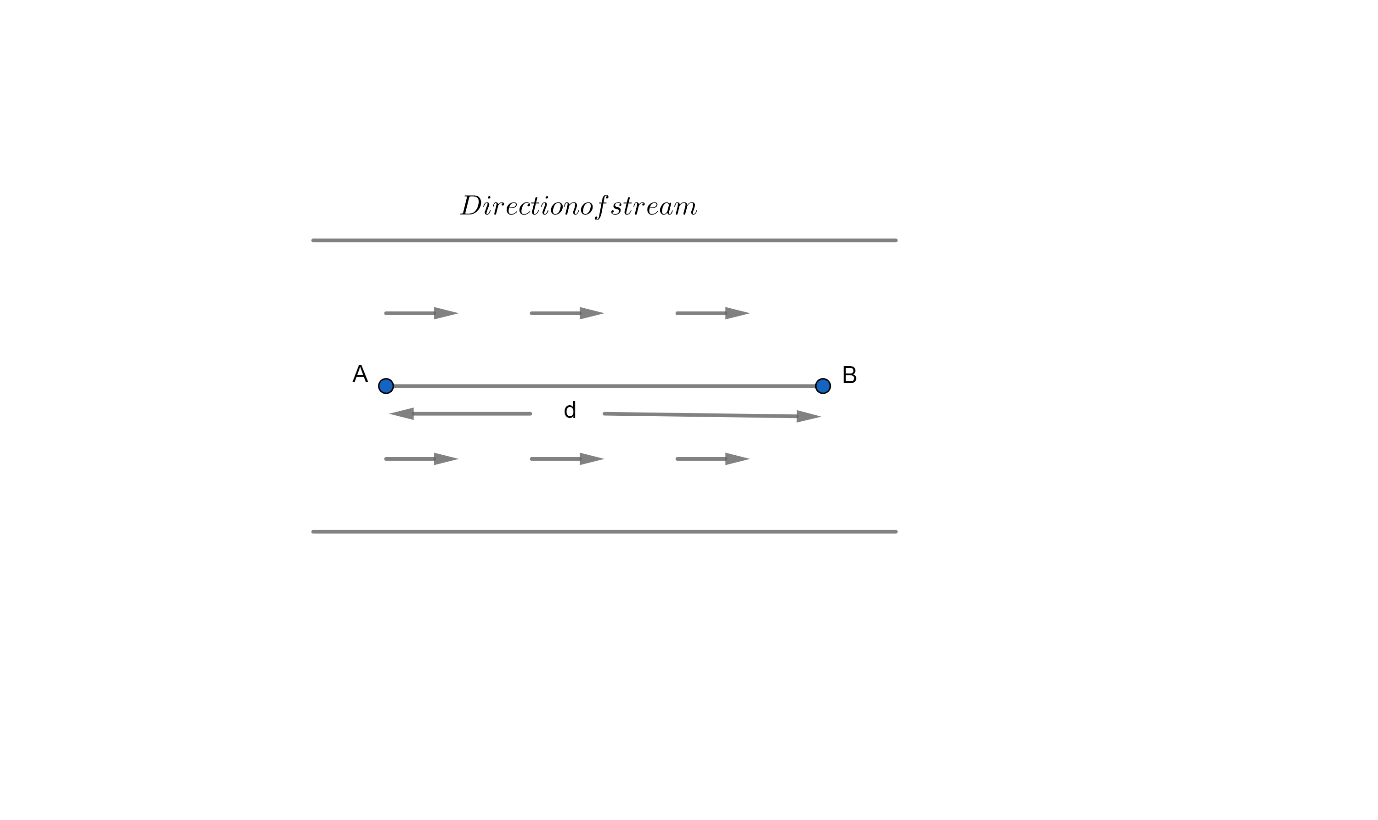
Now, we let the distance AB be d km.
The speed of the boat going from A to B that is downstream$=\left( x+3 \right)km/hr$.
The speed of the boat coming from B to A in upstream$=\left( x-3 \right)km/hr$.
Now, we know that the formula for speed $=\dfrac{\text{distance}}{\text{time}}$.
Now, for downstream we have,
$\begin{align}
  & x+3=\dfrac{d}{1} \\
 & x+3=d.........\left( 1 \right) \\
\end{align}$
Now, for upstream we have,
$\begin{align}
  & \left( x-3 \right)=\dfrac{d}{\dfrac{3}{2}} \\
 & \dfrac{3}{2}\left( x-3 \right)=d.........\left( 2 \right) \\
\end{align}$
Now, we will equate (1) and (2). So, we have,
$\begin{align}
  & x+3=\dfrac{3}{2}\left( x-3 \right) \\
 & 2\left( x+3 \right)=3\left( x-3 \right) \\
 & 2x+6=3x-9 \\
 & 15=x \\
 & x=15km/hr \\
\end{align}$
The speed of a boat in still water is 15 km/hr. Therefore, the correct option is (D).

Note: To solve these types of questions it is important to note that the speed of boat in stream and speed of boat in still water is different in the speed of boat in still water. We add the speed of stream as per the direction of boat and stream.