Question

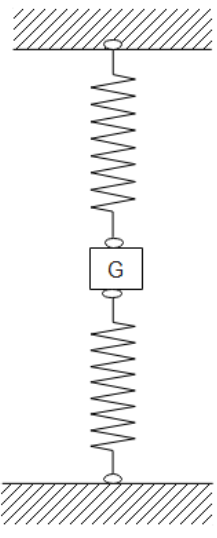
A block tied between two identical springs is in equilibrium. If the upper spring is cut, then the acceleration of the block just after cut is $6m{{s}^{-2}}$. Now if instead of upper string lower spring is cut, then the acceleration of the block just after the cut will be in $m{{s}^{-2}}$ (take g=10)

 

$\begin{align}
  & a)1.25 \\
 & b)4 \\
 & c)10 \\
 & d)2.5 \\
\end{align}$

Answer 1

Hint: Initially, calculate the net displacement of the spring in equilibrium before any spring is cut. The upper spring will stretch because force is exerted in upwards direction. Next, the lower spring will compress to exert force on the body in upward direction. Next calculate the acceleration of the body.

Formulas used:
$\begin{align}
  & kx+mg=ma \\
 & kx=ma-mg \\
 & kx=-4m \\
\end{align}$

Complete answer:
Let us assume x as the displacement in each spring in equilibrium state before any spring is cut. For this situation, the upper spring stretches to exert a force on body in upward direction and lower spring compresses to exert a force on body in upward direction.
$\begin{align}
  & kx+kx=mg \\
 & x=\dfrac{mg}{2k} \\
\end{align}$
Now, when upper spring is cut, forces acting on the body are mg downward and kx in upward direction,
Acceleration will then be equal; to,
$\begin{align}
  & kx+mg-mg=m{{a}_{2}} \\
 & -4m=m{{a}_{2}} \\
 & {{a}_{2}}=4m{{s}^{-2}} \\
\end{align}$
If the lower spring is cut, the forces acting are mg downwards and kx upwards again. Therefore, the acceleration will be $4m{{s}^{-2}}$.

Therefore, the correct option is option b.

Additional information:
In mechanics simple harmonic motions, the force is called a spring force when spring is attached to the body. If the displacement in spring is positive, the resulting por net force acting on the body will be negative. If the displacement in the spring is negative, the resulting force acting on the body is positive. In simple words, spring force on anybody always acts in the direction opposite so that it will restore the body back to the initial position. This can be defined as Newton's laws of motion which tells that a body in rest tends to be at rest and a body in motion tends to be in motion.

Note:
The spring force acts in the direction opposite to the applied force so that object comes back to the same position. The time period of the body oscillating decreases when the spring constant increases. For a given mass, as it accelerates more, it completes its motion faster and in a shorter time period for sure.