Question

: A block rests on a rough inclined plane making an angle of 30 degrees with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block in (kg) is : (Take $g=10m{{s}^{-2}}$)
A. $2$
B. $4$
C. $1.6$
D. $2.5$

Answer 1

Hint:It is given that a block is resting on an inclined plane. This means that the net force on the block is zero. Resolve the forces and find the force acting along the incline and equate it to zero. Then with help of the given data find the mass of the block.

Formula used:
${{F}_{g}}=mg$
Where g is acceleration due to gravity and $m$ is the mass of a body.

Complete step by step answer:
It is given that a block is resting on an inclined plane. This means that the net force on the block is zero.This also means that the force on the block along the incline is zero. Let us calculate the net force on the block. There will be three forces acting on the block and that are the gravitational force in the downwards directional, the normal force exerted by the incline and the frictional force along the incline in the upwards direction, as shown in the figure.

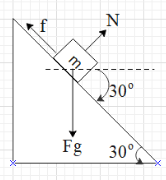
Resolve the gravitational force in the direction of the along the incline and perpendicular to the plane of the incline.

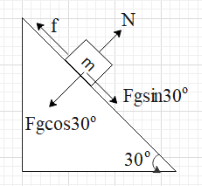
After resolving, we get that the net force on the block in the direction along the incline is ${{F}_{p}}={{F}_{g}}\sin {{30}^{\circ }}-f$.
But ${{F}_{p}}=0$.
$\Rightarrow {{F}_{g}}\sin {{30}^{\circ }}-f=0$
$\Rightarrow f={{F}_{g}}\sin {{30}^{\circ }}$
The gravitational force on a block of mass m is equal to ${{F}_{g}}=mg$, where g is acceleration due to gravity.
And $\sin {{30}^{\circ }}=\dfrac{1}{2}$.
$\Rightarrow f=mg\left( \dfrac{1}{2} \right)=\dfrac{mg}{2}$.
But it is given that the frictional force on the block is 10N.
$\Rightarrow f=10N$.
$\Rightarrow \dfrac{mg}{2}=10$
$\Rightarrow m=\dfrac{20}{g}$.
Substitute $g=10m{{s}^{-2}}$.
$\therefore m=\dfrac{20}{10}=2kg$.
This means that the mass of the block is 2 kg.

Hence, the correct option is A.

Note: Some students make a mistake in this question. They may think that the static frictional force on the force is maximum and write that $f=\mu N$, where $\mu $ is the coefficient of static friction between the block and the plane and N is the normal force exerted on the block. However, it is not necessary that frictional force will be at its limit. It depends on the amount of force (gravitational) exerted on the block along the incline. In this case, the gravitational force along the incline is less than the maximum frictional force possible between the block and the plane.