Question

A block of wood weighing $71.2{\text{ }}N$ and of specific gravity $0.75$ is tied by a string to the bottom of a tank of water in order to have the block totally immersed. What is the tension in the string?

Answer 1

Hint: We will use the formulae of specific gravity and upthrust. Then, we will use the concept of equilibrium and form an equation. Finally, we will evaluate the answer directly by substituting the given values of the parameters involved in the formula.

Formulae used:
$Specific{\text{ }}Density{\text{ }} = {\text{ }}\dfrac{{{\rho _{subs\tan ce}}}}{{{\rho _{Liquid}}}}$
$\Rightarrow Upthrust{\text{ }} = {\text{ }}{V_{subs\tan ce}}{\rho _{Liquid}}g$
\[\Rightarrow V = {\text{ }}\dfrac{M}{\rho }\]
$\Rightarrow W{\text{ }} = {\text{ }}Mg$

Complete step by step answer:
There will be three forces acting on the block of wood. First is the tension in the string acting downwards. Then is the weight of the wood acting downwards.And then the upthrust due to the liquid acting upwards. We can depict this diagrammatically as follows.

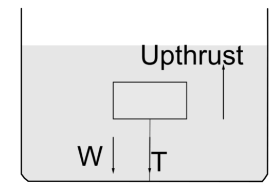
We know that specific gravity is defined as the ratio of density of an object to the density of the liquid. Thus,
$\dfrac{{{\rho _{block}}}}{{{\rho _{liquid}}}}{\text{ }} = {\text{ }}0.75{\text{ }} - - - - - - - - - - - - - {\text{ }}(i)$
We are given weight of the block as
$W{\text{ }} = {\text{ }}71.2{\text{ }}N{\text{ }} - - - - - - - - - {\text{ }}(ii)$
As the system I is in equilibrium.Thus,
$W{\text{ }} + {\text{ }}T{\text{ }} = {\text{ }}upthrust$
Using equation $(ii)$, we get
$71.2{\text{ }} + {\text{ }}T{\text{ }} = {\text{ }}upthrust$
Further, we get
$T{\text{ }} = {\text{ }}upthrust{\text{ }} - {\text{ }}71.2$
We know,
$Upthrust{\text{ }} = {\text{ }}{V_{subs\tan ce}}{\rho _{Liquid}}g$

Thus,
$T{\text{ }} = {\text{ }}{V_{block}}{\rho _{Liquid}}g{\text{ }} - {\text{ }}71.2$
Also we know,
\[V = {\text{ }}\dfrac{M}{\rho }\]
Thus, we get
$T{\text{ }} = {\text{ }}\dfrac{{{M_{block}}}}{{{\rho _{block}}}}{\rho _{Liquid}}g{\text{ }} - {\text{ }}71.2{\text{ }} - - - - - - - {\text{ }}(iii)$
But, from $(i)$, we know
$\dfrac{{{\rho _{block}}}}{{{\rho _{liquid}}}}{\text{ }} = {\text{ }}0.75$
Thus,
$\dfrac{{{\rho _{liquid}}}}{{{\rho _{block}}}}{\text{ }} = {\text{ }}\dfrac{1}{{0.75}}$
Thus, using this value in $(iii)$, we get
\[T{\text{ }} = {\text{ }}\dfrac{{{M_{block}}}}{{0.75}}g{\text{ }} - {\text{ }}71.2{\text{ }} - - - - - {\text{ }}(iv)\]

Now, we know
$W{\text{ }} = {\text{ }}Mg$
$ \Rightarrow W{\text{ }} = {\text{ }}{M_{block}}g$
Thus, using this in $(iv)$, we get
\[T{\text{ }} = {\text{ }}\dfrac{{71.2}}{{0.75}}{\text{ }} - {\text{ }}71.2\]
$ \Rightarrow {\text{ }}T{\text{ }} = {\text{ }}71.2{\text{ }}\left( {\dfrac{1}{{0.75}}{\text{ }} - {\text{ }}1} \right)$
Thus, we get
$T{\text{ }} = {\text{ }}71.2{\text{ }} \times {\text{ }}\dfrac{1}{3}$
Finally, we get
$\therefore T{\text{ }} = {\text{ }}23.74{\text{ }}N$

Hence, the tension in a string is 23.74 N.

Additional Information: Here, we can see that the block is immersed in the liquid without getting totally sunk. Thus, from the knowledge of buoyancy or upthrust and density comparison, we can easily say that the density of the block is nearly the same as that of the liquid. This is also evident from the value of the specific gravity of the block as it is $0.75$ which means that the density of the block is $75\% $ equal to the density of the liquid.

Note: Students should be cautious while manipulating the formulas. Students commit errors while manipulating the formula of weight with the formula of upthrust and thus they have to be very careful while doing so.