Question

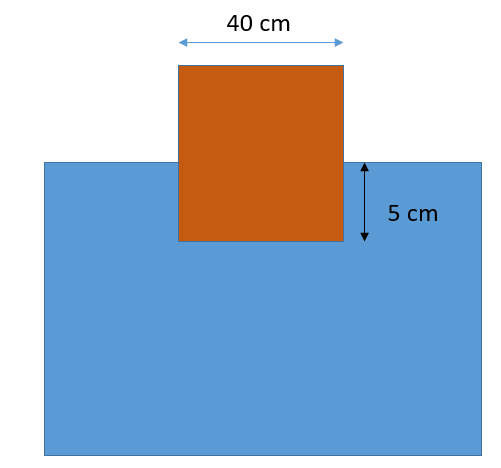
A block of wood side 40cm floats in water in such a way that its lower face is 5cm below the free surface of water. What is the weight of the blocks?

A. 64Kg
B. 16Kg
C. 8 Kg
D. Cannot be determined as the density of wood is not given.

Answer 1

Hint: To solve this problem we used the Archimedes principle which states that the upward buoyant force exerted on a body is immersed in a fluid is equal to the weight of the fluid that the body displaces. Archimedes' principle describes how things can float on water.

Complete step by step answer:
We can see that in the figure given above, the wooden block is submerged partially in the water.
So the volume of the wooden box part that is submerged is
${V_s} = L \times B \times H$
Here ${V_s}$ is the volume of the submerged portion of the block, L and B are the length and breadth of the submerged portion which is equal to 40 cm each respectively. And the Height of the submerged portion is H=5cm.
\[ \Rightarrow {V_s} = \left( {40\;{\rm{cm}} \times 40\;{\rm{cm}} \times 5\;{\rm{cm}}} \right)\]
\[ \Rightarrow {V_s} = \left( {40 \times 40 \times 5} \right){\rm{c}}{{\rm{m}}^3} \times \dfrac{{{{10}^{ - 6}}{{\rm{m}}^{\rm{3}}}}}{{1\;{\rm{c}}{{\rm{m}}^3}}}\]
\[ \Rightarrow {V_s} = \left( {40 \times 40 \times 5} \right) \times \dfrac{{{{10}^{ - 6}}{{\rm{m}}^{\rm{3}}}}}{1}\]
We know that density of water is ${\rho _w} = {10^3}{\rm{Kg/}}{{\rm{m}}^3}$
We know that the Weight of the wooden block is W=Mg where M is the mass of the block and $g$ is the acceleration due to gravity.
We know that the weight of water displaced by the wooden block is given by, ${W_1} = {V_s} \times {\rho _w} \times g$ and here ${V_s}$ is the volume of the submerged portion of the block, ${\rho _w}$ is the density of water and g is the acceleration due to gravity.
Now by using Archimedes principle, we can say that,
Weight of wooden block = weight of water displaced
$Mg{\rm{ }} = {\rm{ }}{V_{im}} \times {\rho _w} \times g$
$M{\rm{ }} = {\rm{ }}(40 \times 40 \times 5){\rm{ }} \times {10^{ - 6}}{m^3} \times {10^3}Kg/{m^3}$.
$M{\rm{ }} = {\rm{ }}8kg$

Therefore, the weight of the block is 8kg. Hence, option (C) is the correct option.

Additional information:
The buoyant force depends on the mass of the object and weight of the object, but it is independent of the density of the liquid. The flotation of the object is always dependent on the Buoyant force. The buoyant force must be negative, positive, and neutral.

Note:
In today’s life, Archimedes' principle is very useful to calculate the volume of the object which has an irregular shape. It can also be determined the density and specific gravity of the object. When the object is submerged, it weighs less because the Buoyant force pushes the object in an upward direction. Mostly Archimedes principle describes the behaviour of any body and in any type of a fluid, whether it is ship or balloon.