Question

A block of metal measuring $ 50cm \times 50cm \times 60cm $ is rolled into a thin strip $ 600m $ long and $ 1mm $ thick. Find the width of the strip in centimetres.

Answer 1

Hint: As we know that the above given question is a word problem. A problem is a mathematical question written as one sentence or more describing a real life scenario where that problem needs to be solved by the way of mathematical calculation. So we have been given the length, breadth and height of a metal block which can be the shape of a cuboid, so we will calculate the volume of this metal or cuboid. We know the formula of the volume of cuboid is $ Volume = length \times breadth \times height $ .

Complete step by step solution:
We need to first understand the requirement of the question which is the breadth of the new formed shape. Let us first draw the diagram of the metal block :

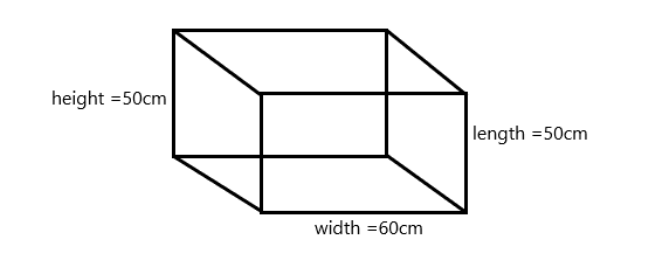
We should note that if this metal block is rolled into a thin strip completely, then the volume of both the materials will be same i.e. Volume of block $ = $ Volume of strip.
We can calculate the volume of block first i.e.
 $ Volume = length \times breadth \times height $ .
So by putting the values we have
 $ V = 50 \times 50 \times 60 $ . It gives us the volume of block $ = 150000c{m^3} $ .
Now we can find the volume of the strip with the same formula.
We have length $ = 600m $ and height $ = 1mm $ . First we need to convert them both into $ cm $ .
We know that $ 1m = 100cm $ , so $ 600m = 600 \times 100cm $ . It gives us length $ = 60000cm $ .
Similarly $ 1mm = \dfrac{1}{{10}}cm $ . So we can calculate the thickness in cm i.e. $ \dfrac{1}{{10}} = 0.1cm $ .
And let us assume the width of the strip be $ x $ .
So we can write Volume of block $ = $ Volume of strip.
By substituting the values we have
 $ 150000 = 60000 \times 0.1 \times x $ .
By transferring all the terms to LHS except $ x $ , we have
 $ x = \dfrac{{150000}}{{6000 \times 0.1}} $ .
It can also be written as $ x = \dfrac{{150000 \times 10}}{{60000 \times 1}} $ .
On solving it gives us the value $ x = 25 $ .
Hence the required width of the strip is $ 25 $ cm.
So, the correct answer is “ $ 25 $ cm”.

Note: We should remember that volume will always be the same if the same block is converted into any shape or size, only the length, height and width can be different. Also the total surface area of a cuboid is $ 2(lb + bh + lh) $ , where $ l,b,h $ are length, breadth and height respectively. Based on the requirement and by observing all the necessary information that is already available in the question we gather the information and then create an equation or by unitary method whichever is applicable, then we solve the problem and then verify the answer by putting the value in the problem and see whether we get the same answer or not.