Question

A block of mass \[M\] is pulled along a horizontal frictionless surface by rope of mass \[m\] by applying a force \[P\] at one end of the rope. The force which the rope exerts on the block is
(A) \[\dfrac{{PM}}{{M - m}}\]
(B) \[\dfrac{{MP}}{{M + m}}\]
(C) \[\dfrac{{pm}}{{M + m}}\]
(D) \[P\]

Answer 1

Hint:Consider Newton's third law of motion; recall the concept of action-reaction pair.There is a reaction force that is present when we apply a force on the block.The whole system will move with a single acceleration.We can use the free body diagram of the rope.

Complete step by step answer:
Consider the Newton’s second law of motion,
\[force(f) = mass \times acceleration(a)\]
Force (\[P\]) is applied at the end of the rope, the other end is attached with the block.
And mention that there is a frictionless surface, so we can neglect the frictional force contribution.
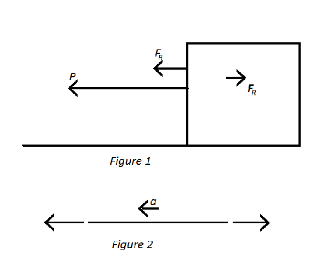
The figure\[1\]has shown the block mass \[M\] is attached with a rope having mass \[m\] pulled by the rope with a force\[P\].
There is a force \[{F_B}\]is acting on the block at the end of rope, there is also a reactive force coming from the block is
\[{F_R} = \dfrac{{(M + m)P}}{{M + m}} - \dfrac{{mP}}{{M + m}} = \dfrac{{MP}}{{M + m}}\]
\[{F_R} = {F_B}\]
The whole system has same acceleration and denoted by \[a\]
Acceleration is equal to the total applied force divided by total mass.
Total mass \[ = m + M\]
Applied force \[ = P\]
Acceleration \[a = \dfrac{P}{{M + m}}\]
Consider figure\[2\], the free body diagram of rope is shown.
From this,
The reaction force is opposite to the applied force, so the difference is,
\[P - {F_R} = mass \times acceleration\]
Substitute the acceleration of rope and mass. Then,
\[P - {F_R} = m \times \dfrac{P}{{M + m}}\]
Rearrange the equation,
\[P - {F_R} = \dfrac{{mP}}{{M + m}}\]
\[{F_R} = P - \dfrac{{mP}}{{M + m}}\]
\[{F_R} = \dfrac{{(M + m)P}}{{M + m}} - \dfrac{{mP}}{{M + m}} = \dfrac{{MP}}{{M + m}}\]
From action-reaction pair, so that these reaction force from the box is equal to the force applied by the end of the rope, in equation,
\[{F_R} = {F_B}\]
\[{F_B} = \dfrac{{MP}}{{M + m}}\]
 So the answer is (B) \[\dfrac{{MP}}{{M + m}}\]

Note:Always remember following points in order to solve such type of problems:
1)Action reaction is always paired.
2)Easy to solve this kind of problem with a free body diagram.
3)Any force can equate to product mass of mass and acceleration.