Question

A block of mass m is pulled along a horizontal surface by applying a force at an angle $\theta $ with the horizontal. If the block travels at a uniform velocity and has a displacement d and the coefficient of friction is $\mu $, then the work done by the applied force is?

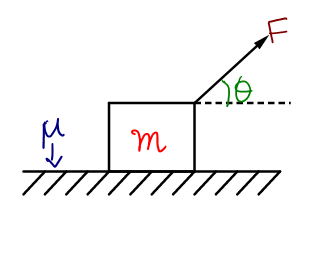
(A). $\dfrac{\mu mgd}{\cos \theta +\mu \sin \theta }$
(B). $\dfrac{\mu mgd\cos \theta }{\cos \theta +\mu \sin \theta }$
(C). $\dfrac{\mu mgd\sin \theta }{\cos \theta +\mu \sin \theta }$
(D). $\dfrac{\mu mgd\cos \theta }{\cos \theta -\mu \sin \theta }$

Answer 1

- Hint: The force acting on the block is at an angle $\theta $ from the horizontal, so the force will be having horizontal and vertical components. Also the frictional force is present. Drawing all the forces acting on the block will give an idea of various forces.

Complete step-by-step solution -

To get a basic idea of what all forces are acting on the block of mass m, we will represent all the forces acting on the block in a diagram,

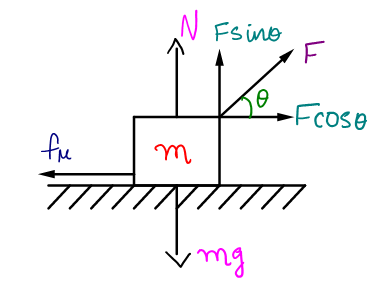
\[\text{F}\] - Force acting at an angle $\theta $ with the horizontal.
$\text{F}\cos \theta $- Component of F acting along the horizontal.
$\text{F}\sin \theta $- Component of F acting along the vertical.
N- Normal force acting on the block
mg- Force due to gravity acting downwards.
${{\text{f}}_{\text{ }\!\!\mu\!\!\text{ }}}$- Frictional force acting against the motion of the body.
When we consider the forces along the vertical direction, we get,
$\text{N}+\text{F}\sin \theta =\text{mg}$ …. equation (1)
If we consider the forces along the horizontal direction, we get,
${{\text{f}}_{\text{ }\!\!\mu\!\!\text{ }}}=\text{F}\cos \theta $ ……. equation (2)
As the body is moving with constant velocity, the frictional force is equal to the horizontal component of force F.
We know that the frictional force acting on a body is equal to the coefficient of friction times the normal force acting on the body.
${{f}_{\mu }}=\mu N$
From equation (1), we can get an expression for N as $\text{N}=\text{mg}-\text{Fsin }\!\!\theta\!\!\text{ }$ and substituting this value in the above equation we get,
${{\text{f}}_{\text{ }\!\!\mu\!\!\text{ }}}=\mu (\text{mg}-\text{F}\sin \theta \text{)}$

Substituting value of ${{\text{f}}_{\text{ }\!\!\mu\!\!\text{ }}}$ in equation (2), we get,
$\text{ }\!\!\mu\!\!\text{ (mg}-\text{Fsin }\!\!\theta\!\!\text{ })=\text{Fcos }\!\!\theta\!\!\text{ }$
$\text{ }\!\!\mu\!\!\text{ mg}=\text{F}\left( \text{cos }\!\!\theta\!\!\text{ }+\text{ }\!\!\mu\!\!\text{ sin }\!\!\theta\!\!\text{ } \right)$
So the force F acting on the block is given by,
$\text{F}=\dfrac{\mu mg}{(\cos \theta +\mu \sin \theta )}$ …… equation (3)
So the work done in moving the block through a distance d is given by,
$\text{W}=\overrightarrow{F}\cdot \overrightarrow{d}$
$\therefore \text{ W}=\dfrac{\mu mgd\cos \theta }{\cos \theta +\mu \sin \theta }$
So the answer to the question is option (B)- $\dfrac{\mu mgd\cos \theta }{\cos \theta +\mu \sin \theta }$

Note: If no external force acts on a system in constant, the system moves with constant velocity. There can be internal forces present, but they cancel out each other in these systems.
Frictional forces are non-conservative forces which means the work done by this force depends on the path followed by the system. It is also known as a dissipative force since it dissipated energy from the system mainly in the form of heat.