Question

A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force P is applied at the free end of the rope, then what is the force exerted by the rope on the block?
$
  {\text{A}}{\text{. }}\dfrac{{{\text{PM}}}}{{{\text{M}} + {\text{m}}}} \\
  {\text{B}}{\text{. }}\dfrac{{{\text{PM}}}}{{{\text{M}} - {\text{m}}}} \\
  {\text{C}}{\text{. }}\dfrac{{{\text{Pm}}}}{{{\text{M}} + {\text{m}}}} \\
  {\text{D}}{\text{. }}\dfrac{{{\text{Pm}}}}{{{\text{M}} - {\text{m}}}} \\
 $

Answer 1

Hint- Here, we will proceed by firstly considering the block and the rope together as one system and applying Newton’s second law of motion to find the acceleration of the block. Then, again applying the same law to find the force exerted by the rope on the block.

Formula Used: Newton’s second law of motion i.e., External Force applied to the system = (Mass of the system)$ \times $(Acceleration of the system).

Complete Step-by-Step solution:

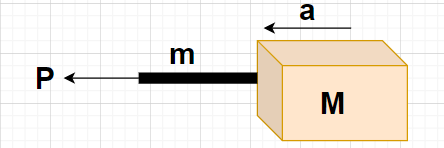
We have a block of mass M placed on a horizontal frictionless surface (i.e., no frictional force is experienced by the block). A rope of mass m whose one end is attached to the block and at the other end (i.e., free end), a force P is applied as shown in the figure.
Let us consider the block and the rope together as the system. Then, we can say that the force P is the only external force applied to the system. Let us suppose that a is the acceleration which this system is having.
Here, Mass of the system = M+m
External force applied to system = P
According to Newton’s second law of motion, we have
External Force applied to the system = (Mass of the system)$ \times $(Acceleration of the system)
$
   \Rightarrow {\text{P}} = \left( {{\text{M}} + {\text{m}}} \right) \times {\text{a}} \\
   \Rightarrow {\text{a}} = \dfrac{{\text{P}}}{{{\text{M}} + {\text{m}}}} \\
 $
Since, the acceleration of the block and rope will be same as that of the acceleration of the system (i.e., $\dfrac{{\text{P}}}{{{\text{M}} + {\text{m}}}}$) because they both are attached together.
Acceleration of the block = $\dfrac{{\text{P}}}{{{\text{M}} + {\text{m}}}}$
For the block of mass M when considered separately the only external force applied to it will be that exerted by the rope on the block.
By applying Newton’s second law of motion on the block of mass M, we can write
Force exerted by the rope on the block = (Mass of the block)$ \times $(Acceleration of the block)
$ \Rightarrow $ Force exerted by the rope on the block = ${\text{M}}\left( {\dfrac{{\text{P}}}{{{\text{M}} + {\text{m}}}}} \right) = \dfrac{{{\text{PM}}}}{{{\text{M}} + {\text{m}}}}$
Therefore, option A is correct.

Note- In this particular problem, there was no friction involved. But, if we had a surface which wasn’t frictionless then, the frictional force between the surface and the block needs to be considered. Also, friction force is considered as an external force so the net external force on the system will be the sum of frictional force and the force applied (P).