Question

A block of mass m is kept over another block of mass M and the system rests on a horizontal surface. A constant horizontal force F acting on the lower block produces acceleration $\dfrac{F}{{2\left( {m + M} \right)}}$ in the system, the two blocks always move together. (a) Find the coefficient of kinetic friction between the bigger block and the horizontal surface. (b) Find the frictional force acting on the smaller block. (c) Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system.

Answer 1

Hint: In order to solve this question we need to find out the net frictional force acting on the system. The net force will be calculated by taking both the masses and using the acceleration provided in question. The coefficient of friction is equal to the divide of net force acting on the system to the normal. Frictional force is equal to the product of mass of the block and acceleration provided to it.

Step by step solution:
Step 1:
The question has three parts. We are going to solve these questions part by part
Given: A block of mass m is kept over another block of mass M and the system rests on a horizontal surface and a constant horizontal force F acting on the lower block produces acceleration $\dfrac{F}{{2\left( {m + M} \right)}}$ in the system.
So by this information we will make a diagram based on it:

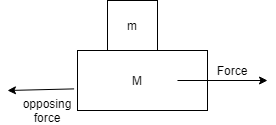
(c) The work done by the force of friction on the smaller block by the bigger block during a displacement d of the system.
We are told that blocks move together that means the acceleration of both the blocks will be the same. So we will treat both the block as a system of mass m+M.
Now suppose there is opposing force acting against the force and is denoted by${F_m}$
Acceleration given in the question is$\dfrac{F}{{2\left( {m + M} \right)}}$, from this we will find out the force acting which is F=ma
Net force will be ${F_{NET}}$=F−${F_m}$=(m+M)×a
a) The coefficient of kinetic friction between the bigger block and the horizontal surface
The both blocks are moving with each other that’s why there will be no static friction.
Then the frictional force for the bigger block is given as${F_M} = \mu N$where,$\mu $ is the coefficient of kinetic friction and N is the normal acting on the system
We can write this equation as${F_M} = \mu \left( {m + M} \right)g$ …… (2)
From equation 1 ${F_M} = \dfrac{F}{2}$
Now, equating both the equation for the coefficient of kinetic friction, $\dfrac{F}{2} = \mu \left( {m + M} \right)g$
This will give us the value of coefficient of kinetic friction$\mu = \dfrac{F}{{2\left( {m + M} \right)g}}$
a) The frictional force acting on the smaller block:

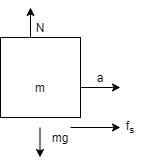
In the diagram the block of mass m has acceleration (a) and is getting a frictional force${f_s}$ due to the bigger block of mass M and there is no net force acting on the system. N is the normal and acts opposite to mg.
Then the frictional force be represented as${f_s} = m \times a$
Substituting the value of acceleration given in the question we get, ${f_s} = m \times \dfrac{F}{{2\left( {m + M} \right)g}}$
This implies, the frictional force acting on the smaller block is${f_s} = m \times \dfrac{F}{{2\left( {m + M} \right)g}}$
Substituting the value of acceleration we get, ${F_{NET}}$=(m+M)× $\dfrac{F}{{2\left( {m + M} \right)}}$
The masses get cancel out and we will get net frictional force will be$\dfrac{F}{2}$…….. (1)
Now, work done by the force of friction on the smaller block by the bigger block during a displacement d of the system is ${F_{NET}} \times d \times \cos \theta $
So again substituting the value of net force we get, ${\left( {{W_f}} \right)_M} = \dfrac{F}{2} \times d \times \cos \left( {{{180}^0}} \right)$
The angle between the acting force and opposing frictional force is opposite to each other that’s why ${180^0}$
On solving for work done we get, ${\left( {{W_f}} \right)_M} = - \dfrac{{Fd}}{2}$ as$\cos {180^0} = - 1$

Note:Friction is the resistance to motion of one object moving relative to another. It is not a fundamental force. This is the reason it is acting opposite to the force applied on the system and coefficient of friction is defined as the ratio of the force required to move two sliding surfaces over each other, and the force holding them together.