Question

A block of mass $m$ is kept on a plank. The coefficient of friction between the plank and block is 1. The plank is slowly raised from one end so that it makes an angle with horizontal. the forces of friction acting on the plank, when $\theta =30{}^\circ $ and $\theta =60{}^\circ $ are respectively
A. $\dfrac{mg}{2},\dfrac{mg}{2}$
B. $\dfrac{\sqrt{3}}{2}mg,\dfrac{mg}{2}$
C. $\dfrac{mg}{2},\dfrac{\sqrt{3}}{2}mg$
D. $mg,mg$

Answer 1

Hint: Here, we need to find the expression of the frictional force. The expression can be found by resolving the forces acting on the body into their components. Finally, we will equate the frictional force with the balancing force to find the answer.

Formula used:
$\alpha ={{\tan }^{-1}}(\mu )$
$f=mg\sin \theta $

Complete answer:
Here, the different types of forces acting on the box can be visualized with the help of the following diagram:

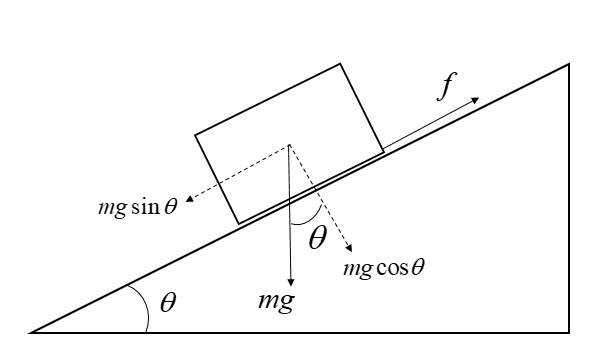
Also, in the question it is given that the coefficient of friction between the body and the plank is 1. This can be written as:
$\mu =1$
Hence, the angle of repose can be found using equation: $\alpha ={{\tan }^{-1}}(\mu )$ ---(i)
Hence, here, $\alpha ={{\tan }^{-1}}(1)=45{}^\circ $
We know that as long as the angle of inclination of the plank remains below the angle of repose, and the body is at rest, the expression for the force of friction acting on the body is given by:
$f=mg\sin \theta $ ------(ii)
Hence, for $\theta =30{}^\circ $:
Frictional force acting on the body = ${{f}_{1}}=mg\sin 30$
$\Rightarrow {{f}_{1}}=mg\times \dfrac{1}{2}=\dfrac{mg}{2}$
Also, as soon as the angle of the plank increases beyond the angle of repose, the expression for the frictional force becomes:
$f=mg\cos \theta $ --------(iii)
Hence, for , $\theta =60{}^\circ $:
Frictional force acting on the body =${{f}_{2}}=mg\cos 60$
$\Rightarrow {{f}_{2}}=mg\times \dfrac{1}{2}=\dfrac{mg}{2}$
Hence, in both the cases, i.e., in case of $\theta =30{}^\circ $ and $\theta =60{}^\circ $, the frictional force acting on the body is the same.

So, the correct answer is “Option A”.

Note:
Write the expression for the frictional force carefully. The frictional force acting on the body kept on a plank depends on the inclination of the plank. The expressions for frictional force are different and depend upon whether the angle of inclination is less or more than the angle of repose.