Question

A block of mass m is in rest with respect to a rough incline kept in elevator moving up with acceleration:

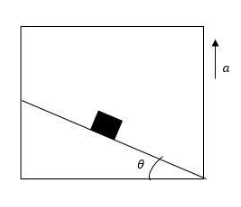
A. The contact force between block and incline is parallel to the incline.
B. The contact force between block and incline is of the magnitude $m(g + a)$
C. The contact force between block and incline is perpendicular to the incline
D. The contact force is of the magnitude $mg \cos \theta $

Answer 1

Hint:In this question,we are going to apply the concept of contact forces. Contact forces are forces that act between two objects that are physically touching each other.

Complete step by step answer:

$\therefore ma$ pseudo force acting between the blocks.
$\therefore $The block is perpendicular to the inclined angle therefore,
$N = m(a + g)\cos \theta $ . . . . (i)
And this is one first equation Now, along the inclined plane the force is equal to,
$f = m(a + g)\sin \theta $ . . . . (ii)
So, by contact force$ = \sqrt {{N^2} + {F^2}} $ . . . . (iii)
Put (i) and (ii) on equation (iii)
So, contact force $ = \sqrt {(m(ag)\cos {\theta ^2} + {{(m(a + g)\sin \theta )}^2}} $
$ = \sqrt {(m{{(a + g)}^2}{{\cos }^2}\theta + {m^2}{{(a + g)}^2}{{\sin }^2}\theta } $
$ = \sqrt {({m^2}{{(a + g)}^2}(\cos {\theta ^2} + \sin {\theta ^2}} $
$ = m(a + g)\sqrt {{{\cos }^2}\theta + {{\sin }^2}\theta } $
$ = m(a + g) \times 1$
$ = m(a + g)$
Through, the contact force between block incline is of the magnitude is $m(g + a)$
Therefore, the correct option is (B) The contact force between block and incline is of the magnitude $m(g + a)$.

Note:The meaning of pseudo is fake or false. So overall it is a fake force.Let us understand a simple definition of it. If a body of mass ‘m’ is placed in a non-inclined frame (like bus, train or car) having an acceleration ‘a’, then pseudo force is acting in a direction opposite to the vehicle.
$\overrightarrow F pseudo = - m\overrightarrow a $
Example: Traveling in a bus, train or car etc.