Question

A block of mass \[m\] is connected to two springs of spring constant \[2k\] and \[k\] respectively as shown in vertical plane. At equilibrium both springs are compressed by the same lengths. If suddenly the lower spring is cut what is the acceleration of the block just after spring is cut?

A.\[2g\] downward
B.\[2g\] downward
C.\[2g\] upward
D. none of these

Answer 1

Hint:Use the expression for Newton’s second law of motion and formula for spring force. Apply Newton’s second law of motion to the system of block and spring in the vertical direction and determine the value of spring force on upper spring. Apply Newton’s second law of motion to the spring-block system when the lower spring is cut to determine the acceleration of the block.

Formulae used:
The expression for Newton’s second law of motion is
\[{F_{net}} = ma\] …… (1)
Here, \[{F_{net}}\] is net force on the object, \[m\] is mass of the object and \[a\] is acceleration of the object.
The spring force \[F\] is given by
\[F = kx\] …… (2)
Here, \[k\] is spring constant and \[x\] is displacement of the spring.

Complete step by step answer:
We have given that a block of mass \[m\] is attached to two springs of spring constants \[2k\] and \[k\] respectively. The free body diagram of the given system of block and springs is as follows:

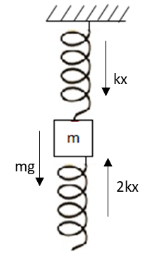
In the above free body diagram, \[mg\] is the weight of the block acting in the downward direction, spring force \[kx\] of upper spring acting in downward direction and spring force \[2kx\] of lower spring acting in upward direction.

At equilibrium, both the springs are compressed by the same length \[x\].Apply Newton’s second law to the block-spring system in the vertical direction.
\[ - kx - mg + 2kx = 0\]
\[ \Rightarrow kx = mg\]
When the lower spring is cut then also the weight of block and spring force of the upper spring will remain the same and this new system will have an acceleration.
Apply Newton’s second law to the new block-spring system in the vertical direction.
\[ - kx - mg = ma\]
Substitute \[mg\] for \[kx\] in the above equation.
\[ - mg - mg = ma\]
\[ \therefore a = - 2g\]
Therefore, the acceleration of the block just after the spring is cut is \[2g\] in the downward direction.

Hence, the correct option is A.

Note:The students may think how we determined the direction of the acceleration of the block is in downward direction. We can see that the acceleration of the block we determined has a negative sign which shows that the acceleration of the block is in the downward direction.