
A block of mass \[M\] has a circular cut with a frictionless surface as shown. The block rests on the horizontal frictionless surface of a fixed table. Initially the right edge of the block is at \[x = 0\] , in a coordinate system fixed to the table. A point mass \[m\] is released from rest at the topmost point of the path as shown and it slides down. When the mass loses contact with the block, its position is \[x\] and the velocity is \[v\] . At that instant, which of the following options is/are correct?
A. The velocity of the block $ M $ is $ V = - \dfrac{m}{M}\sqrt {2gR} $
B. The $ x $ component of displacement of the center of mass of the block $ M $ is: \[ - \dfrac{{mR}}{{M + m}}\]
C. The position of the point mass is \[x = - \sqrt 2 \dfrac{{mR}}{{M + m}}\]
D. The velocity of the point mass \[m\] is \[v = \sqrt {\dfrac{{2gR}}{{1 + \dfrac{m}{M}}}} \]

Answer
585.9k+ views
Hint: Start by drawing a well-labeled diagram for the initial position of the two bodies and another diagram showing the final position of the two. Then use the concept of conservation of linear momentum (i.e. \[M{V_1} = m{v_2}\] ) and conservation of energy (i.e. Initial Potential energy = Final kinetic energy of block of mass M + Final kinetic energy of point mass m) to find the velocity of the block. Then use the concept of center of mass (Equation - \[\Delta {x_{COM}} = \dfrac{{\Delta m{x_1} + \Delta M{x_2}}}{{m + M}}\] )
Complete step-by-step answer:
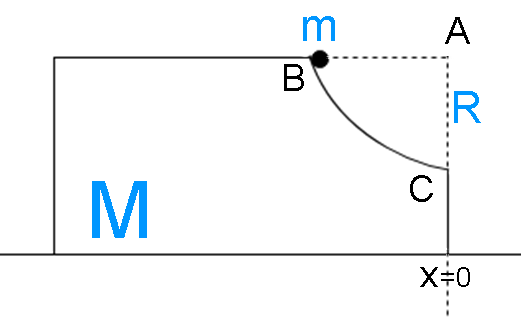
The diagram of the given situation is given below
Redrawing the diagram for the point when point mass is about to lose contact with the block.

By using the concept of conservation of energy, we know
Before moving on to the mathematical equations, we must remember that there is no external force involved. So the concept of conservation of energy (energy can neither be created nor destroyed, but can only change from one form to another) and concept of conservation of momentum (the momentum in a closed system is always considered).
Initial Potential energy = Final kinetic energy of block of mass M + Final kinetic energy of point mass m
\[ \Rightarrow mgR = \dfrac{1}{2}MV_1^2 + \dfrac{1}{2}mv_2^2\]
\[ \Rightarrow mgR = \dfrac{1}{2}MV_1^2 \times \dfrac{M}{M} + \dfrac{1}{2}mv_2^2\]
\[ \Rightarrow mgR = \dfrac{{{M^2}V_1^2}}{{2M}} + \dfrac{1}{2}mv_2^2\] (Equation 1)
By using the concept of conservation of momentum, we know
\[M{V_1} = m{v_2}\] (Equation 2)
Replacing the value of \[M{V_1}\] obtained from equation 2 in equation 1, we get
\[ \Rightarrow mgR = \dfrac{{{{(m{v_2})}^2}}}{{2M}} + \dfrac{1}{2}mv_2^2\]
\[ \Rightarrow gR = \dfrac{{m{v_2}^2}}{{2M}} + \dfrac{1}{2}v_2^2\]
\[ \Rightarrow gR = \dfrac{{m{v_2}^2 + Mv_2^2}}{{2M}}\]
\[ \Rightarrow m{v_2}^2 + Mv_2^2 = 2MgR\]
\[ \Rightarrow v_2^2 = \dfrac{{2MgR}}{{m + M}}\]
\[ \Rightarrow v_2^2 = \dfrac{{2gR}}{{1 + \dfrac{m}{M}}}\]
\[ \Rightarrow {v_2} = \sqrt {\dfrac{{2gR}}{{1 + \dfrac{m}{M}}}} \]
Let’s assume that the block of mass M moves by a distance \[y\] when the point mass loses contact with the block and it is given in the problem that the point mass is at distance \[x\] from the origin when it loses contact with the block.
We know that the center of mass of a closed system does not move when no external force is applied. So \[\Delta {x_{COM}} = 0\]
We also know that \[x\] coordinate of the center of mass of the whole system is given by
\[\Delta {x_{COM}} = \dfrac{{\Delta m{x_1} + \Delta M{x_2}}}{{m + M}}\]
\[ \Rightarrow 0 = \dfrac{{m(R - y) + My}}{{m + M}}\]
\[ \Rightarrow My = - m(R - y)\]
\[ \Rightarrow My = - mR + my\]
$ y = - \dfrac{{mR}}{{m + M}} $
Hence, option B and D are the correct choices.
Note – To find the \[x\] component of displacement, we used the concept of center of mass. In the concept of center of mass we assume that all the mass is situated in a single point that depends on the mass and distance of each of the individual points. It is similar to the situation, where we assume the whole charge of the spherical body is concentrated at the center.
Complete step-by-step answer:
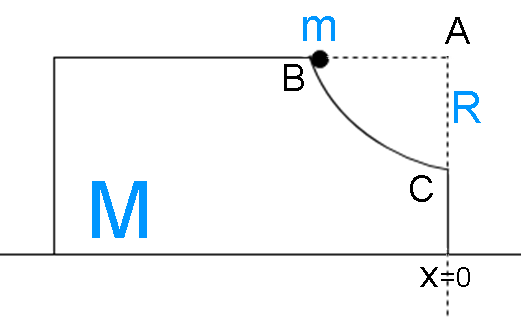
The diagram of the given situation is given below

Redrawing the diagram for the point when point mass is about to lose contact with the block.

By using the concept of conservation of energy, we know
Before moving on to the mathematical equations, we must remember that there is no external force involved. So the concept of conservation of energy (energy can neither be created nor destroyed, but can only change from one form to another) and concept of conservation of momentum (the momentum in a closed system is always considered).
Initial Potential energy = Final kinetic energy of block of mass M + Final kinetic energy of point mass m
\[ \Rightarrow mgR = \dfrac{1}{2}MV_1^2 + \dfrac{1}{2}mv_2^2\]
\[ \Rightarrow mgR = \dfrac{1}{2}MV_1^2 \times \dfrac{M}{M} + \dfrac{1}{2}mv_2^2\]
\[ \Rightarrow mgR = \dfrac{{{M^2}V_1^2}}{{2M}} + \dfrac{1}{2}mv_2^2\] (Equation 1)
By using the concept of conservation of momentum, we know
\[M{V_1} = m{v_2}\] (Equation 2)
Replacing the value of \[M{V_1}\] obtained from equation 2 in equation 1, we get
\[ \Rightarrow mgR = \dfrac{{{{(m{v_2})}^2}}}{{2M}} + \dfrac{1}{2}mv_2^2\]
\[ \Rightarrow gR = \dfrac{{m{v_2}^2}}{{2M}} + \dfrac{1}{2}v_2^2\]
\[ \Rightarrow gR = \dfrac{{m{v_2}^2 + Mv_2^2}}{{2M}}\]
\[ \Rightarrow m{v_2}^2 + Mv_2^2 = 2MgR\]
\[ \Rightarrow v_2^2 = \dfrac{{2MgR}}{{m + M}}\]
\[ \Rightarrow v_2^2 = \dfrac{{2gR}}{{1 + \dfrac{m}{M}}}\]
\[ \Rightarrow {v_2} = \sqrt {\dfrac{{2gR}}{{1 + \dfrac{m}{M}}}} \]
Let’s assume that the block of mass M moves by a distance \[y\] when the point mass loses contact with the block and it is given in the problem that the point mass is at distance \[x\] from the origin when it loses contact with the block.
We know that the center of mass of a closed system does not move when no external force is applied. So \[\Delta {x_{COM}} = 0\]
We also know that \[x\] coordinate of the center of mass of the whole system is given by
\[\Delta {x_{COM}} = \dfrac{{\Delta m{x_1} + \Delta M{x_2}}}{{m + M}}\]
\[ \Rightarrow 0 = \dfrac{{m(R - y) + My}}{{m + M}}\]
\[ \Rightarrow My = - m(R - y)\]
\[ \Rightarrow My = - mR + my\]
$ y = - \dfrac{{mR}}{{m + M}} $
Hence, option B and D are the correct choices.
Note – To find the \[x\] component of displacement, we used the concept of center of mass. In the concept of center of mass we assume that all the mass is situated in a single point that depends on the mass and distance of each of the individual points. It is similar to the situation, where we assume the whole charge of the spherical body is concentrated at the center.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




