Question

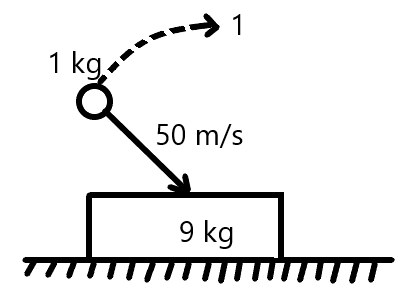
A block of mass $ 9\,kg $ is lying on a rough horizontal surface. A particle of mass $ 1\,kg $ strikes the block with a speed of $ 50\,m{s^{ - 1}} $ at an angle of $ 37 $ with the vertical and sticks to it. The frictional coefficient between the ground and the block is $ \mu = 0.4 $ . Find the velocity of the combined system just after the collision assuming limiting friction coefficient between the block and the ground after the collision?

Answer 1

Hint : Here, in the solution we will consider two cases. In the first case, the angular velocity of the block will be zero. On the other hand, in the second case, the angular velocity of the block will be $ $ 0.4\, $ $ . Here, we will use the change in momentum relation to find the velocity of the combined system.

Complete Step By Step Answer:
Case 1: if $ \mu = 0 $

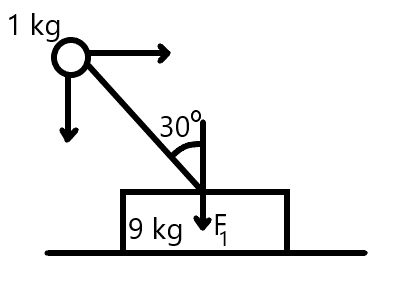
Then the momentum will change by the block in collision and is given by
 $ {f_2}\Delta t = 9V $
Now, the momentum conservation in x-direction is given by
 $ 1 \times 50\,\sin 37^\circ = \left( {9 + 1} \right)V $
 $ \Rightarrow \,V = 3\,m{\operatorname{s} ^{ - 1}} $
Now, putting this value in the above equation we get
 $ {f_2}\Delta t = 9 \times 3 $
 $ \Rightarrow \,{f_2}\Delta t = 27 $
Now, the change in momentum of the block in y-direction by the ball is given by
 $ {f_1}\Delta t = 30\,\cos 37^\circ $
 $ \Rightarrow \,{f_1}\Delta t = 40 $
Case 2: when collision time $ \Delta t $ will be very small than $ \mu = 0.4 $ .

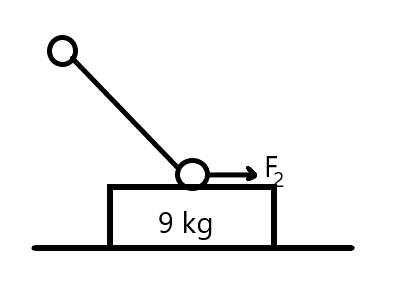
Now, the frictional force acting on the block is, $ {f_s} = \left( {{f_1} + \log } \right)\mu $
Now in this case, the change in momentum of the block in x-direction will be $ 9V' $ and is given by
 $ \left( {{f_2} - {f_s}} \right)\Delta t = 9V' $
 $ \Rightarrow \,\left( {{f_2} - \left( {{f_1} + \log } \right)\mu } \right)\Delta t = 9V' $
 $ \Rightarrow \,\left( {{f_2}\Delta t - \left( {{f_1}\Delta t + \log \Delta t} \right)\mu } \right) = 9V' $
 $ \Rightarrow \,27 - \left( {40} \right)\left( {0.4} \right) = 9V' $
 $ \Rightarrow \,27 - 16 = 9V' $
 $ \Rightarrow \,11 = 9V' $
 $ \Rightarrow \,V' = \dfrac{{11}}{9} $
 $ \Rightarrow \,V' \simeq 1.2\,m{s^{ - 1}} $
Therefore, the velocity of the combined system just after the collision will be approximately equal to $ 1.2\,m{s^{ - 1}} $ .

Note :
Here, $ \mu = 0 $ is the value of angular velocity before the collision and $ \mu = 0.4 $ is the value of the angular velocity after the collision. That is why, we have considered two cases here, that is, the case before collision and the case after collision. Also, the force $ {F_1} $ is in perpendicular direction and the force $ {F_2} $ is in horizontal direction.