Question

 A block of mass 5 kg is (1) pushed in case (A) and (2) pulled in case (B), by force \[F=20N\], making an angle of \[30{}^\circ \] with the horizontal, as shown in the figures. The coefficient of friction between the block and floor is \[\mu =0.2\]. The difference between the accelerations of the block, in case (B) and case (A) will be: \[(g=10m{{s}^{-2}})\]

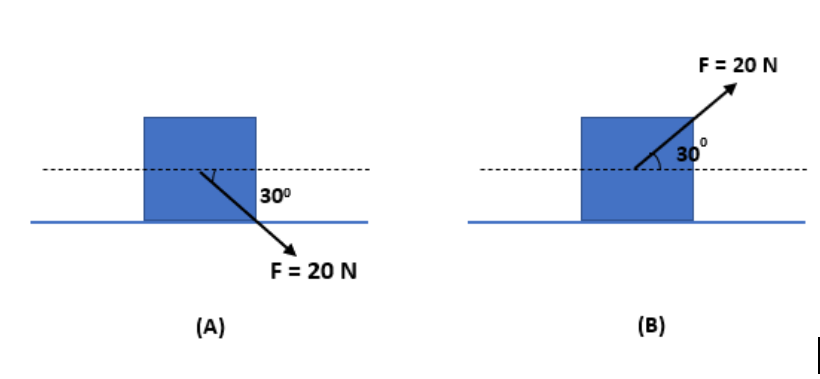
A. \[0m{{s}^{-2}}\]
B. \[0.8m{{s}^{-2}}\]
C. \[0.4m{{s}^{-2}}\]
D. \[3.2m{{s}^{-2}}\]

Answer 1

Hint: Frictional force is the product of the coefficient of friction and normal force. Here we are applying force in two ways and along with an angle to the horizontal surface. So we have to split this force into vertical and horizontal components to find the vertically and horizontally acting forces on the blocks. From this, we can find the acceleration of the blocks.
Formula used:
\[F=ma\], where m is the mass and a is the acceleration.
\[f=\mu N\], where f is the frictional force, \[\mu \] is the coefficient of friction and N is the normal force.

Complete step by step answer:
 

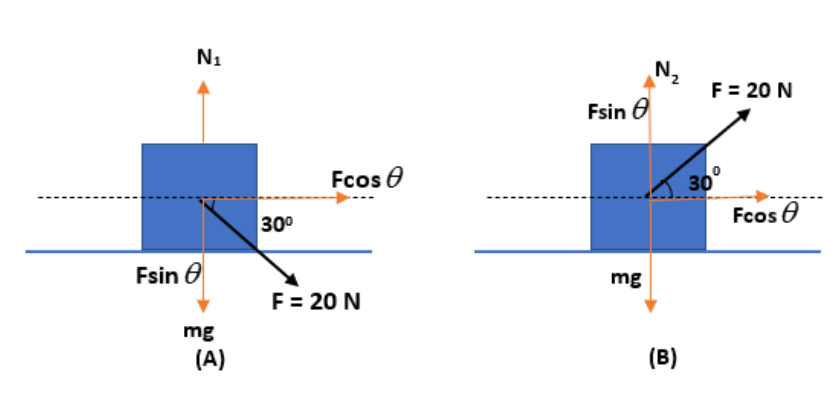
First, we can consider the case A. We are trying to push the block of mass 5 kg with a force 20 N. But we are pushing the block with an angle \[30{}^\circ \] to the horizontal. We can split this force into two so that we can find the normal force. The force can be split into \[F\cos \theta \] and \[F\sin \theta \]. Here the force is 20 N and the angle is \[30{}^\circ \]. Thus,
Normal force, \[{{N}_{1}}=F\sin \theta +mg\]
Here, weight and vertical components of force are acting in the same direction. So that they will be added up.
Here \[mg=5\times 10=50N\]
\[{{N}_{1}}=10\sin 30{}^\circ +50\]
To find the frictional force (f) we have to multiply the normal force with the coefficient of friction between the block and the floor.
\[f={{N}_{1}}\times 0.2\]
\[f=60\times 0.2=12N\]
This frictional force has to be minimised from the horizontal force to find the actual force on the block.
So, the pushing force on the block in the direction of motion is,
\[=20\times \cos 30{}^\circ =17.32N\]
The acceleration of the block will be equal to the ratio of actual force to the mass of the block.
\[\begin{align}
  & {{a}_{1}}=\dfrac{17.32N-12N}{5kg} \\
 & {{a}_{1}}=1.064m{{s}^{-2}} \\
\end{align}\]
Next, we can consider the second case B. Here we are pulling the block with an angle \[30{}^\circ \] to the horizontal. So we have to split the force to find the normal force and force along the horizontal line.
Normal force, \[{{N}_{2}}=mg-20\sin 30{}^\circ \]
Here the weight is acting opposite to the vertical component of the force that we applied. That’s why we are using a negative sign instead of a positive sign here.
\[{{N}_{2}}=50-10=40N\]
To find the frictional force we have to multiply with the normal force acting on the block.
\[f=0.2\times 40N\]
\[f=8N\]
This frictional have to be minimised from the force acting on the horizontal line to get the actual force. Thus,
\[=20\times \cos 30{}^\circ -8N=17.32N-8N\]
The acceleration of this block can be determined from the ratio of the actual force on the block to the mass of the block.
\[{{a}_{2}}=\dfrac{17.32N-8N}{5kg}\]
\[{{a}_{2}}=1.864m{{s}^{-2}}\]
So the change in acceleration will be equal to,
\[{{a}_{2}}-{{a}_{1}}=1.864-1.064\]
\[{{a}_{2}}-{{a}_{1}}=0.8m{{s}^{-2}}\]
Hence the option B is correct.
Note: The splitting of the resultant force is important. Because the difference in acceleration is developed only because of the vertical component of the force. During pushing, this force is in the same direction of weight of the block. But during pulling, this vertical component is in the opposite direction of weight of the block. It is advised to use diagrams for the easy calculation of this kind of problems.