
A block of mass 4 kg is released from a height of 25 cm on a smooth track. The minimum value of h, so that it completes the vertical circle should be
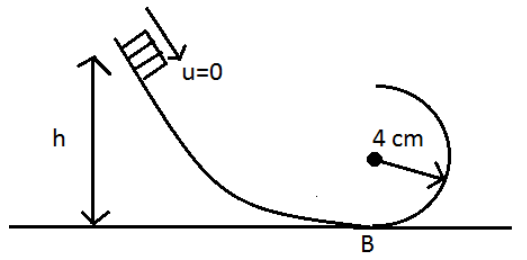
A. 25 cm
B. 10 cm
C. 20 cm
D. 5 cm

Answer
570.6k+ views
Hint: Before proceeding with the solution, we must get through with the principle of conservation of mechanical energy as it is the key part of the approach of finding the solution.
The principle of the conservation of mechanical energy states that the total mechanical energy in a system (i.e., the sum of potential and kinetic energies) remains constant as long as the only forces acting are conservative forces i.e. the value of mechanical energy does not equal to zero ever.
The principle of the conservation of mechanical energy would help us in proceeding with the solution of the given question as the potential energy of the object at height $h$is equal to the kinetic energy possessed by the same object when $h=0$and thus equating them would provide us the correct solution.
Complete answer:
Applying conservation of energy at the top and bottom points, we could derive the speed of the object at the bottom $v=\sqrt{5gr}$
Thus, for the block to complete vertical circle, its minimum speed should be $\sqrt{5gr}$
And from the law of Conservation of mechanical energy,
Potential Energy at the top = Kinetic energy at the bottom
$\Rightarrow mgh=\dfrac{1}{2}m{{v}^{2}}$
Putting the value of v
$\Rightarrow gh=\dfrac{1}{2}{{\left( \sqrt{5gr} \right)}^{2}}$
$\Rightarrow gh=\dfrac{1}{2}5gr$
$\Rightarrow h=\dfrac{5}{2}r$
Putting the value of r
$\Rightarrow h=\dfrac{5}{2}\times 4$
$\therefore h=10cm$
Therefore the minimum value of $h=10cm$
Hence the correct option would be (B) 10cm.
Note:
While using the Law of conservation of mechanical energy, one must keep in mind that potential energy is equal to the kinetic energy of the object only if the object travels from a height h to $h=0$. And also, proper conversion of the unit must also be taken care of when required.
The principle of the conservation of mechanical energy states that the total mechanical energy in a system (i.e., the sum of potential and kinetic energies) remains constant as long as the only forces acting are conservative forces i.e. the value of mechanical energy does not equal to zero ever.
The principle of the conservation of mechanical energy would help us in proceeding with the solution of the given question as the potential energy of the object at height $h$is equal to the kinetic energy possessed by the same object when $h=0$and thus equating them would provide us the correct solution.
Complete answer:
Applying conservation of energy at the top and bottom points, we could derive the speed of the object at the bottom $v=\sqrt{5gr}$
Thus, for the block to complete vertical circle, its minimum speed should be $\sqrt{5gr}$
And from the law of Conservation of mechanical energy,
Potential Energy at the top = Kinetic energy at the bottom
$\Rightarrow mgh=\dfrac{1}{2}m{{v}^{2}}$
Putting the value of v
$\Rightarrow gh=\dfrac{1}{2}{{\left( \sqrt{5gr} \right)}^{2}}$
$\Rightarrow gh=\dfrac{1}{2}5gr$
$\Rightarrow h=\dfrac{5}{2}r$
Putting the value of r
$\Rightarrow h=\dfrac{5}{2}\times 4$
$\therefore h=10cm$
Therefore the minimum value of $h=10cm$
Hence the correct option would be (B) 10cm.
Note:
While using the Law of conservation of mechanical energy, one must keep in mind that potential energy is equal to the kinetic energy of the object only if the object travels from a height h to $h=0$. And also, proper conversion of the unit must also be taken care of when required.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




