Question

A block of mass 2 kg is free to move along the x axis. It is initially at rest and from t=0 seconds onwards, the block is subjected to a time dependent force f (t) in the x direction. The force f (t) varies with t. Find the kinetic energy of the block after 4.5 seconds?

Answer 1

Hint: The kinetic energy of the block depends on the linear momentum and the mass of the block. The kinetic energy of the block can be determined as the ratio of the square of the change in linear momentum to that of the mass of the block.

 Formula Used:
The formula for calculating the kinetic energy is:
$KE = \dfrac{{p_f^2 - p_i^2}}{{2m}}$

Complete step by step answer:

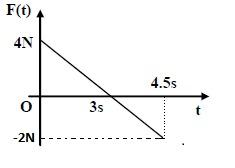
The situation that is provided in the question can be described by drawing the force time graph as:
The area under the force time graph gives the change in the momentum of the block.
Area under the f(t) graph = Area of triangle ABO – Area of triangle DCO
$
  A = \dfrac{1}{2} \times 4 \times 3 - \dfrac{1}{2} \times 2 \times 1.5 \\
   = 4.5\,N.s \\
 $
As the block is initially at rest, so the initial kinetic energy is zero. And the area denotes the final kinetic energy of the block.
The formula for calculating the kinetic energy is:
$KE = \dfrac{{p_f^2 - p_i^2}}{{2m}}$
Put the value of pf =4.5 N.s, m=2 kg and pi =0 N.s in the above equation.
 $
  KE = \dfrac{{{{\left( {4.5} \right)}^2} - {{\left( 0 \right)}^2}}}{{2\left( 2 \right)}} \\
   = 5.06\,{\text{J}} \\
 $

Hence, the kinetic energy of the block is 5.06 J

Note:
The area under the force time graph gives the change in the momentum (product of mass and velocity) of the body from which the final kinetic energy of the body can be determined using the provided formula.