Question

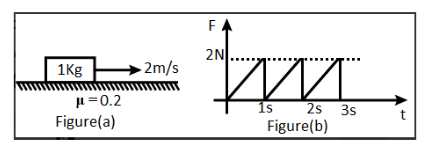
A block of mass $ 1kg $ is moving at $ t = 0 $ with speed $ 2m{s^{ - 1}} $ on a rough horizontal surface with coefficient of friction $ 0.2 $ . A horizontal force $ F $ is applied in the same direction of velocity which varies with time as shown in figure (b). Find the speed of the block at $ t = 3s\left( {g = 10m{s^{ - 2}}} \right) $ .

 $ \left( A \right)1m{s^{ - 1}} \\
  \left( B \right)zero \\
  \left( C \right)5m{s^{ - 1}} \\
  \left( D \right)2m{s^{ - 1}} \\ $

Answer 1

Hint: In order to solve this question, we are going to first see the values and the intervals for the force and the acceleration depending upon the graph that is given in the question. After that, from the acceleration, the velocity is found by integrating it and then, the correct option is chosen.
The net force on the block can be given from the equation
$ ma = F - \mu gm $

Complete step by step solution:
From the figures given in the question, the inferences that can be drawn are:
$ f =
  2t [t < 1 ] \\
  2\left( {t - 1} \right) [1 < t < 2] \\
  2\left( {t - 2} \right) [2 < t < 3] \\ $
The net force on the block can be given from the equation
$ ma = F - \mu gm \\
  a = \dfrac{F}{m} - \mu g \\ $
Thus, the conditions imposed on the acceleration can be taken as:
$ a =
  2t [ t < 1 ] \\
  2\left( {t - 1} \right) [ 1 < t < 2 ] \\
  2\left( {t - 2} \right) [ 2 < t < 3 ] \\ $
Now, integrating the acceleration to find the velocity of the particle, we get
$ \int\limits_2^v {\dfrac{{dv}}{{dt}} = \int\limits_0^1 {2\left( {t - 1} \right)dt + } } \int\limits_1^2 {2\left( {t - 2} \right)dt + } \int\limits_2^3 {2\left( {t - 3} \right)dt} \\
   \Rightarrow v - 2 = \left( {{t^2} - 2t} \right)\left| {_0^1} \right. + \left( {{t^2} - 4t} \right)\left| {_1^2} \right. + \left( {{t^2} - 6t} \right)\left| {_2^3} \right. \\ $
On further solving, we get
$ v - 2 = \left( {1 - 2} \right) + \left( {4 - 80 + \left( {1 - 4} \right)} \right) \\
   \Rightarrow v - 2 = \left( { - 1} \right) + \left( { - 1} \right) + \left( { - 1} \right) \\
   \Rightarrow v - 2 = - 3 \\
   \Rightarrow v = - 1m{s^{ - 1}} \\ $
Now, as we know that the friction is a secondary adjusting force and it will not increase the velocity in the direction. Hence, the velocity turns zero after a time interval.
So, the option $ \left( B \right)zero $ is the correct answer.

Note:
The coefficient of friction, µ, is a measure of the amount of friction existing between two surfaces. A low value of coefficient of friction indicates that the force required for sliding to occur is less than the force required when the coefficient of friction is high. Here the value for the coefficient is given equal to $ 0.2 $ .