Question

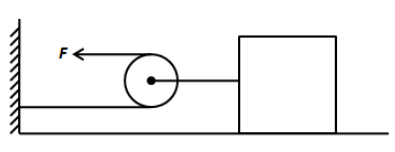
A block of mass 180 kg is to be pulled such that it moves with an acceleration of \[2\,{\text{m/}}{{\text{s}}^2}\] (as shown in figure). What would be the value of force F for such motion to take place on a smooth surface?

A. 180 N
B. 360 N
C. 720 N
D. Zero

Answer 1

Hint: When the free end of the rope is pulled with some force, the tension develops in the lower arm of the rope. The tension in the lower arm of the rope is exactly equal to the force applied to pull the free end. Therefore, the double amount of force is developed when the force F is applied to the free end. Using Newton’s second law of motion, determine the value of force F.

Formula used:
Newton’s second law, \[F = ma\]
where, m is the mass and a is the acceleration.

Complete step by step answer:
In the given system, we can see the rope goes over the pulley such that its one end is connected to the rigid support and the other end is free. The free end can be pulled so that the block moves towards the left. When the free end of the rope is pulled with some force, the tension develops in the lower arm of the rope. We can easily infer that the tension in the lower arm of the rope is exactly equal to the force applied to pull the free end. We can draw the free body diagram as follows,

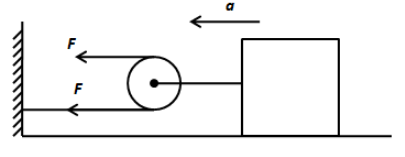
Using Newton’s second law, we can write,
\[2F = ma\]
\[ \Rightarrow F = \dfrac{{ma}}{2}\]
Substituting \[m = 180\,{\text{kg}}\] and \[a = 2\,{\text{m/}}{{\text{s}}^2}\] in the above equation, we get,
\[F = \dfrac{{\left( {180} \right)\left( 2 \right)}}{2}\]
\[ \therefore F = 180\,{\text{N}}\]
Therefore, the force required to move the block is 180 N.

So, the correct answer is option A.

Note: The direction of the tension force is always directed towards the rigid support and hence in the above figure we have shown the direction of tension towards the left. The pulley arrangements always ease the efforts required to pull the body since the required force is reduced by the tension in the rope. We have assumed that the mass of the rope is negligible as compared to the mass of the block.