Question

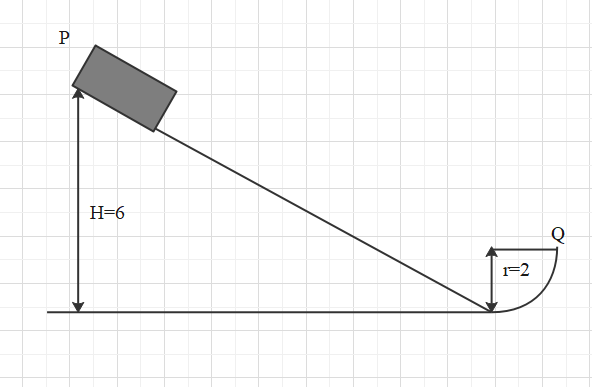
A block of mass 1 kg is released from P on a frictionless track which ends in quarter circular track of radius 2 m at the bottom. What is the magnitude of radial acceleration and total acceleration of the block when it arrives at Q?

Answer 1

Hint: Since the block is released from a certain height, so calculate the loss of height. We get the displacement of the object. Then by using the formula: ${{v}^{2}}={{u}^{2}}+2gs$ , find the final velocity of the block. Now, we know that the radial acceleration is given by: ${{a}_{R}}=\dfrac{{{v}^{2}}}{r}$ and tangential acceleration is given by: ${{a}_{T}}=g$ . So, total acceleration is: $a=\sqrt{{{\left( {{a}_{R}} \right)}^{2}}+{{\left( {{a}_{T}} \right)}^{2}}}$ .

Formula used:
${{v}^{2}}={{u}^{2}}+2gs$, where v is final velocity, u is initial velocity, g is the acceleration due to gravity and s is the distance covered.
${{a}_{R}}=\dfrac{{{v}^{2}}}{r}$, where ${{a}_{R}}$is the radial acceleration, v is the velocity and r is the radius.
${{a}_{T}}=g$, where ${{a}_{T}}$ is the tangential acceleration and g is the acceleration due to gravity
$a=\sqrt{{{\left( {{a}_{R}} \right)}^{2}}+{{\left( {{a}_{T}} \right)}^{2}}}$, where a is the total acceleration, ${{a}_{R}}$is the radial acceleration and ${{a}_{T}}$ is the tangential acceleration.

Complete step by step answer:
We have:
$
{{h}_{1}}=6m \\
{{h}_{2}}=2m \\
u=0m/s \\
m=1kg \\
$
So, the displacement of the block is:
$
\Rightarrow s=\left( 6-2 \right) \\
\Rightarrow s=4m
$
Now, by using the Newton’s law of motion: ${{v}^{2}}={{u}^{2}}+2gs$
We get:
$
\Rightarrow {{v}^{2}}=0+\left( 2\times 9.81\times 4 \right) \\
\Rightarrow {{v}^{2}}=78.48{{m}^{2}}{{s}^{-2}}
$
 As we know that:
The radial acceleration is given by: ${{a}_{R}}=\dfrac{{{v}^{2}}}{r}$
So, we have:
$
\Rightarrow {{a}_{R}}=\dfrac{78.48}{2} \\
\Rightarrow {{a}_{R}}=39.2m{{s}^{-2}}
$
So, total acceleration is:
$
\Rightarrow a=\sqrt{{{\left( {{a}_{R}} \right)}^{2}}+{{\left( {{a}_{T}} \right)}^{2}}} \\
\Rightarrow a=\sqrt{{{\left( 39.2 \right)}^{2}}+{{\left( 9.81 \right)}^{2}}} \\
\therefore a=40.4m{{s}^{-2}}
$

Note:
We have been given a block that is at rest and then it accelerates as it is released from the point P. The block is released from a certain height therefore its potential energy is converted into kinetic energy. So, by conserving the total energy, we can write:
$
\Delta PE=\Delta KE \\
\implies -mg\left( {{h}_{2}}-{{h}_{1}} \right)=\dfrac{1}{2}m\left( {{v}^{2}}-{{u}^{2}} \right) \\
\implies \left( 6-2 \right)=\dfrac{1}{2}{{v}^{2}} \\
\therefore 78.48={{v}^{2}}
$