Question

A block kept on a rough surface starts sliding when the inclination of the surface is (θ) with respect to the horizontal. The coefficient of static friction between the blocks and the surface is:
$\begin{align}
  & A.\text{ sin}\theta \\
 & \text{B}\text{. tan}\theta \\
 & \text{C}\text{. cos}\theta \\
 & \text{D}\text{. sec}\theta \\
\end{align}$

Answer 1

Hint: We have been provided with a block which is sliding on an inclined plane with an angle θ. Draw the diagram and resolve the forces and components of forces. Forces normal to the plane are balanced and when the body just begins to slide, force which is parallel to the plane is balanced. Frictional force is given by $F=\mu N$ add this expression and put the values from the balanced equation and calculate the coefficient of static friction.

Formula used: Frictional force acting on the body is given by, $F=\mu N$
Where F=frictional force, μ = coefficient of static friction, N = normal force.

Complete step by step answer:

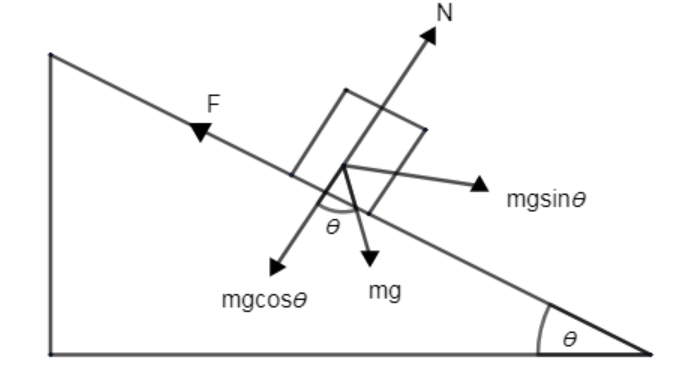
The question stated that a block of mass (m) is kept on a rough surface. A free body diagram for the given scenario is shown in the figure. When the inclination of the surface is θ with respect to the horizontal, the block starts slipping. When the block of mass (m) was slipping, a frictional force acts between the block and inclined surface in the opposite direction of that of the slipping of the block.
Now let’s resolve the force which is acting on the block of mass (m) as you can see in the figure, normal N acts perpendicular to the block. Consider while mg is acting downwards. Since mg is not aligned in either the x-axis or in the y-axis. Therefore take sine and cosine components of mg. $mg\sin \theta $ component is on right side of mg while $mg\cos \theta $ is on left side of mg because as we know cosine components always take on the direction of θ or in other work we can say that θ angle must be in between mg and $mg\cos \theta $.
As you can see in free body diagram, forces normal to the planes are balanced as the blocks cannot move normal to the plane and therefore normal force (N) balances components of mg which is $mg\cos \theta $ mathematically,
$mg\cos \theta =N.....\left( 1 \right)$
When the body (block) just begins to slide, forces parallel to the plane are balanced, so as you can see in the diagram, static forces (f) balances the sine component of mg. mathematically,
$F=mg\sin \theta ........\left( 2 \right)$
If F is frictional force, μ is coefficient of static frictional of N is normal then frictional force acting when the body just begins to slide is given by,
$F=\mu N.......\left( 3 \right)$
Now substitute$e{{q}^{n}}\left( 1 \right)and\text{ e}{{\text{q}}^{n}}\left( 2 \right)\text{in e}{{\text{q}}^{n}}\left( 3 \right)$, we get,
$\mu mg\cos \theta =mg\sin \theta $
Cancelling m and g on both sides, we get,
$\mu =\tan \theta $
Hence, the coefficient of static friction between the blocks and the surface is $\tan \theta $.

So, the correct answer is “Option B”.

Note: The process of raising one edge over another i.e. keeping another edge fixed, through a certain angle is known as banking of objects. In this question we have used the concept of banking of objects. The angle made by the surface of the plank with horizontal surface is called the angle of banking. The ratio of the maximum static friction force between the surfaces in contact before movement commences to the normal force (N) is called the coefficient of static friction.