Question

A block is pulled a distance x along a rough horizontal table by a horizontal string. If the tension in the string is T, the weight of the block is W, normal reaction is N, and frictional force is F. Write down the work done by each of these forces.

Answer 1

Hint: Here we have given a block which is pulled by a string along a rough horizontal surface. It experiences the forces of gravitational pull, the normal reaction force, frictional force and tension in the string. For all these forces we have to calculate the work done by each force. So first we will draw a simple diagram then using the formula of work done we will solve the question.
Formula used:
\[W=Fd\cos \theta \]

Complete step by step answer:
Let us first draw a simple diagram for the given question.

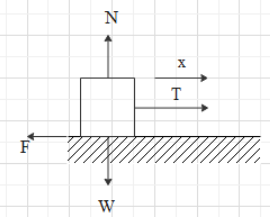
Here the block is pulled along a horizontal surface with a horizontal string. It moves along x direction where x is the distance or here we can say displacement as it is giving as direction. T is the tension in the string, W is the weight or the gravitational pull experienced by the block due to its mass. F is the frictional force as the surface is rough therefore there will be frictional forces acting opposite to the direction of motion. N is the normal reaction force which will act opposite the gravitational pull.
Now work done is given as dot product of force and displacement, it is given as
\[W=Fd\cos \theta \]
Where θ is the angle between force and displacement.
Now, work done by tension can be given as
\[{{W}_{T}}=Tx\cos \theta \]
As we can see from the above diagram, tension T and distance x are in the same direction. And the angle between T and x will be zero. Substituting \[\theta =0\]in above equation we get
\[\begin{align}
  & {{W}_{T}}=Tx\cos 0 \\
 & \Rightarrow {{W}_{T}}=Tx\left( 1 \right) \\
 & \Rightarrow {{W}_{T}}=Tx \\
\end{align}\]
Now the work done by the weight is given as
\[{{W}_{W}}=Wx\cos \theta \]
From the above diagram the angle between x and W will be 90 as they are perpendicular to each other. Substituting \[\cos \theta =90{}^\circ \]in above equation, we get
\[\begin{align}
  & {{W}_{W}}=Wx\cos 90{}^\circ \\
 & \Rightarrow {{W}_{W}}=Wx\left( 0 \right) \\
 & \Rightarrow {{W}_{W}}=0 \\
\end{align}\]
Similarly, work done by the normal force is given as
\[{{W}_{N}}=Nx\cos \theta \]
Normal reaction force N also makes an angle of 90 as it is also perpendicular to the direction of displacement. Substituting \[\cos \theta =90{}^\circ \]in above equation, we get
\[\begin{align}
  & {{W}_{N}}=Nx\cos 90{}^\circ \\
 & \Rightarrow {{W}_{N}}=Nx\left( 0 \right) \\
 & \Rightarrow {{W}_{N}}=0 \\
\end{align}\]
Now considering the frictional force, it is opposite the direction of motion, hence it makes an angle of 180 with the plane or the displacement. And work done by it is given as
\[\begin{align}
  & {{W}_{F}}=Fx\cos \theta \\
 & {{W}_{F}}=Fx\cos 180{}^\circ \\
 & \Rightarrow {{W}_{F}}=Fx\left( -1 \right) \\
 & \Rightarrow {{W}_{F}}=-Fx \\
\end{align}\]
Hence we calculated the work done by each force.

Note:
Weight is often assumed as mass and here mass is also not given. But weight is actually the gravitational force or pull experienced by an object due to the mass of other objects relative to it. Also weight changes with the surface or with relative to which the object experiences the gravitational pull whereas mass remains the same.