Question

A block is placed on top of a smooth inclined plane of inclination $\theta $ kept on the floor of a lift. When the lift is descending with a retardation $a$ the block is released. Find the acceleration of the block relative to the incline.
A) $g\sin \theta $
B) $a\sin \theta $
C) $\left( {g - a} \right)\sin \theta $
D) $\left( {g + a} \right)\sin \theta $

Answer 1

Hint:The acceleration due to gravity is always directed downwards. Here the lift is said to be descending with some retardation. So we consider the effective acceleration due to gravity. The force acting on the book will be directed parallel to the surface of the incline.

Formula used:
-The effective acceleration of a body placed in a lift is given by, ${g_{eff}} = g - a$ where $g$ is the acceleration due to gravity and $a$ is the acceleration of the lift.

Complete step by step answer.
Step 1: Sketch a figure depicting the system under consideration.

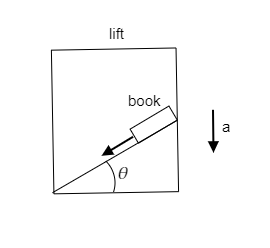
In the above figure, a horizontal surface makes an angle $\theta $ with the floor of the lift. A book is placed on this horizontal surface and when the lift starts to move downwards with retardation $a$, the book is released from the top of the table. We have to determine the acceleration of the book with respect to the incline.
Step 2: Sketch a figure depicting the components of the weight to find the relative acceleration of the book.
The weight of the book if the system did not include a lift is $W = mg$ .
Now as the system includes a descending lift, the weight of the book will be $W = m{g_{eff}}$ . The weight of the book makes the angle $\theta $ . Thus it will have a horizontal component and vertical component.

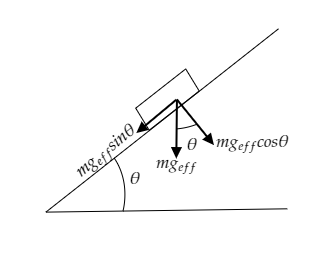
Now, the effective acceleration is given by, ${g_{eff}} = g - \left( { - a} \right) = g + a$ .
Thus we have the weight of the book as $W = m\left( {g + a} \right)$ .
From the above figure, the acceleration of the book with respect to the incline is the component of the effective acceleration along the incline.
i.e., the relative acceleration of the book will be ${g_{eff}}\sin \theta = \left( {g + a} \right)\sin \theta $ .

Thus the correct option is D.

Note:While resolving the weight into its components, the component having the angle $\theta $ in between will be the cosine component and the component without the angle will be the sine component. The acceleration of the incline will be the same as that of the lift retardation. Retardation is defined as the negative acceleration and so we substitute $ - a$ while calculating the effective acceleration due to gravity.