Question

A block B of specific gravity 2 and another block C of specific gravity 0.5. Both are joined together and they are floating inside water such that they are completely dipped inside water, the ratio of the masses of the blocks B and C is
A. 2:1
B. 3:2
C. 5:3
D. 2:3

Answer 1

Hint: We are given two blocks B and C which is dipped in water. The specific gravity of both the blocks is given and it is also said that the blocks are joined together and they are floating in the water. We know the condition in which a body floats in water. By applying this condition we can find the ratio of the masses of the two blocks.

Formula used:
Weight of the body,
$w=mg$
The buoyant force of a body,
${{F}_{B}}=\rho Vg$
Density,
$\rho =\dfrac{M}{V}$

Complete step-by-step solution:
In the question, it is said that two blocks are joined together and completely immersed in water.
Consider the situation as shown in the figure below.

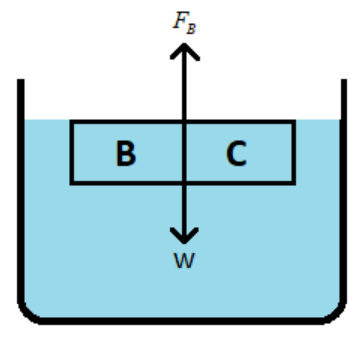
The two blocks joined together are B and C.
It is said that even though the blocks are completely dipped in the water they are floating in the water.
Therefore there are two forces acting on the body; the weight of the body and buoyant force.
Let us consider the weight of the body.
The weight of the full body is the sum of the weight of the blocks B and C.
We know that weight of a body is the product of the mass of that body and earth’s gravity, i.e.
$w=mg$, ‘w’ is the weight of the body, ‘m’ is the mass of the body and ‘g’ is the gravitational acceleration.
Let ‘${{w}_{B}}$’ be the weight of the block B.
Therefore the weight of block B will become,
${{w}_{B}}={{m}_{B}}\times g$, were ‘${{m}_{B}}$’ is the mass of the block B and ‘g’ is gravity.
Now, let ‘${{w}_{C}}$’ be the weight of the block C, then we have,
${{w}_{C}}={{m}_{C}}\times g$, were ‘${{m}_{C}}$’ is the mass of the block C.
Now we have total weight of the body,
$\begin{align}
  & w=\left( {{m}_{B}}\times g \right)+\left( {{m}_{C}}\times g \right) \\
 & w=\left( {{m}_{B}}+{{m}_{C}} \right)g \\
\end{align}$
The other force acting on the body is the buoyant force, ${{F}_{B}}$.
We know that the buoyant force is the weight of the liquid displaced by the body.
Therefore in this case the buoyant force of the total body is the sum of the buoyant force of the block B and C.
Therefore we have,
${{F}_{B}}={{\rho }_{w}}({{V}_{B}}+{{V}_{C}})g$, were ‘${{F}_{B}}$’ is buoyant force, ‘${{\rho }_{w}}$’ is the density of water, ‘${{V}_{B}}$’ is the volume of block B, ‘${{V}_{C}}$’ is the volume of block C and ‘g’ is gravity.
We know that density is mass per unit volume, i.e.
$\rho =\dfrac{M}{V}$ were ‘$\rho $’ is density, ‘M’ is mass and ‘V’ is volume
From the above equation, we can find the volume of block B as,
${{V}_{B}}=\dfrac{{{m}_{B}}}{{{\rho }_{B}}}$
In the question, we are given the specific gravity of block B.
We know that specific gravity is the ratio of the density of a substance and density of water.
We are given the specific gravity of block B to be 2.
Therefore we can write,
$\dfrac{{{\rho }_{B}}}{{{\rho }_{w}}}=2$
Therefore we get the density of block B as,
${{\rho }_{B}}=2{{\rho }_{w}}$
Substituting this in the equation of volume of block B, we get
${{V}_{B}}=\dfrac{{{m}_{B}}}{2{{\rho }_{w}}}$
We are also given the specific gravity of block C to be 0.5.
Similarly we get volume of block C as,
$\begin{align}
  & {{V}_{C}}=\dfrac{{{m}_{C}}}{{{\rho }_{C}}} \\
 & {{V}_{C}}=\dfrac{{{m}_{C}}}{0.5{{\rho }_{w}}} \\
\end{align}$
Now we can write buoyant force of the body as,
$\begin{align}
  & {{F}_{B}}={{\rho }_{w}}({{V}_{B}}+{{V}_{C}})g \\
 & {{F}_{B}}={{\rho }_{w}}\left( \dfrac{{{m}_{B}}}{2{{\rho }_{w}}}+\dfrac{{{m}_{C}}}{0.5{{\rho }_{w}}} \right)g \\
 & {{F}_{B}}=\dfrac{{{\rho }_{w}}}{{{\rho }_{w}}}\left( \dfrac{{{m}_{B}}}{2}+\dfrac{{{m}_{C}}}{0.5} \right)g \\
 & {{F}_{B}}=\left( 0.5{{m}_{B}}+2{{m}_{C}} \right)g \\
\end{align}$
In the question it is said that the body is floating in water.
We know that when a body floats in water, the weight of the body will be equal to the buoyant force.
Therefore,
$w={{F}_{B}}$
We know the values of ‘$w$’ and ‘${{F}_{B}}$’. Substituting this in the above equation,
  \[\begin{align}
  & \left( {{m}_{B}}+{{m}_{C}} \right)g=\left( 0.5{{m}_{B}}+2{{m}_{C}} \right)g \\
 & \left( {{m}_{B}}+{{m}_{C}} \right)=\left( 0.5{{m}_{B}}+2{{m}_{C}} \right) \\
\end{align}\]
Let us take ‘${{m}_{C}}$’ common on both sides of the equation, we get
$\begin{align}
  & {{m}_{C}}\left( \dfrac{{{m}_{B}}}{{{m}_{C}}}+1 \right)={{m}_{C}}\left( \dfrac{0.5{{m}_{B}}}{{{m}_{C}}}+2 \right) \\
 & \left( \dfrac{{{m}_{B}}}{{{m}_{C}}}+1 \right)=\left( \dfrac{0.5{{m}_{B}}}{{{m}_{C}}}+2 \right) \\
 & \dfrac{{{m}_{B}}}{{{m}_{C}}}-\dfrac{0.5{{m}_{B}}}{{{m}_{C}}}=2-1 \\
 & \dfrac{0.5{{m}_{B}}}{{{m}_{C}}}=1 \\
 & \dfrac{{{m}_{B}}}{{{m}_{C}}}=\dfrac{1}{0.5} \\
\end{align}$
Multiplying denominator and numerator with 2 on both sides we get,
$\begin{align}
  & \dfrac{2{{m}_{B}}}{2{{m}_{C}}}=\dfrac{1}{0.5}\times \dfrac{2}{2} \\
 & \dfrac{{{m}_{B}}}{{{m}_{C}}}=\dfrac{2}{1} \\
\end{align}$
Therefore the ratio of the masses of blocks B and C is 2:1
Hence the correct answer is option A.

Note: Here we have two blocks B and C. These two blocks together form the whole body. Hence when we calculate the weight of the body it is the sum of the weight of the two blocks B and C, and the buoyant force of the body is the sum of the buoyant force experienced by the two blocks B and C.
Specific gravity is actually the ratio of the density of the object and a reference substance. Here in this case we take water to be the reference substance. Hence it is the ratio of the density of the object and density of water.