Question

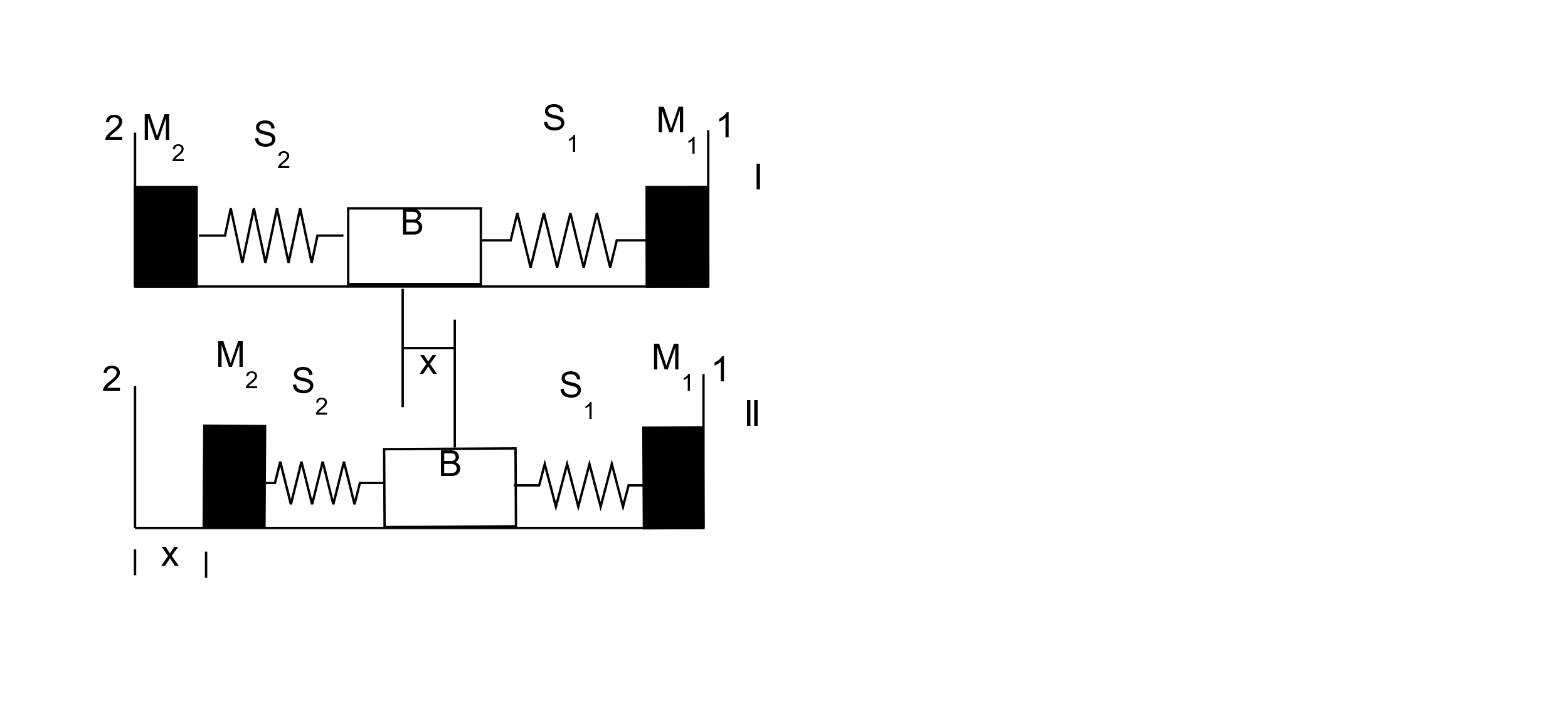
A block (B) is attached to two unstretched springs $ {S_1} $ and $ {S_2} $ with spring constants $ k $ and $ 4k $ respectively (see figure I).The other ends are attached to identical supports $ {M_1} $ and $ {M_2} $ not attached to the walls. The springs and supports have negligible mass. There is no friction anywhere. Block B is displaced towards wall $ 1 $ by a small distance x (figure II) and released. The block returns and moves a maximum distance y towards wall $ 2 $ . Displacements x and y are measured with respect to the equilibrium position of block B. The ratio $ \dfrac{y}{x} $ ​ is:

(A) $ 4 $
(B) $ 2 $
(C) $ \dfrac{1}{2} $
(D) $ \dfrac{1}{4} $

Answer 1

Hint: We are asked to find the ratio $ \dfrac{y}{x} $ . Let us start by redrawing the figure and adding the second displacement onto it. The new figures will give us a rough idea of the question. The velocity of the block in both cases is zero. Here we consider the energies of the spring instead of the velocity of the block.
Potential energy of a spring is given by the formula, $ PE = \dfrac{1}{2}k{x^2} $
Where $ k $ is known as the spring constant or the force constant
 $ x $ is the distance from the equilibrium position

Complete answer:
 We can start by considering the two diagrams as said in the question. The two diagrams (displacement with respect to x and displacement with respect to y) will be as follows

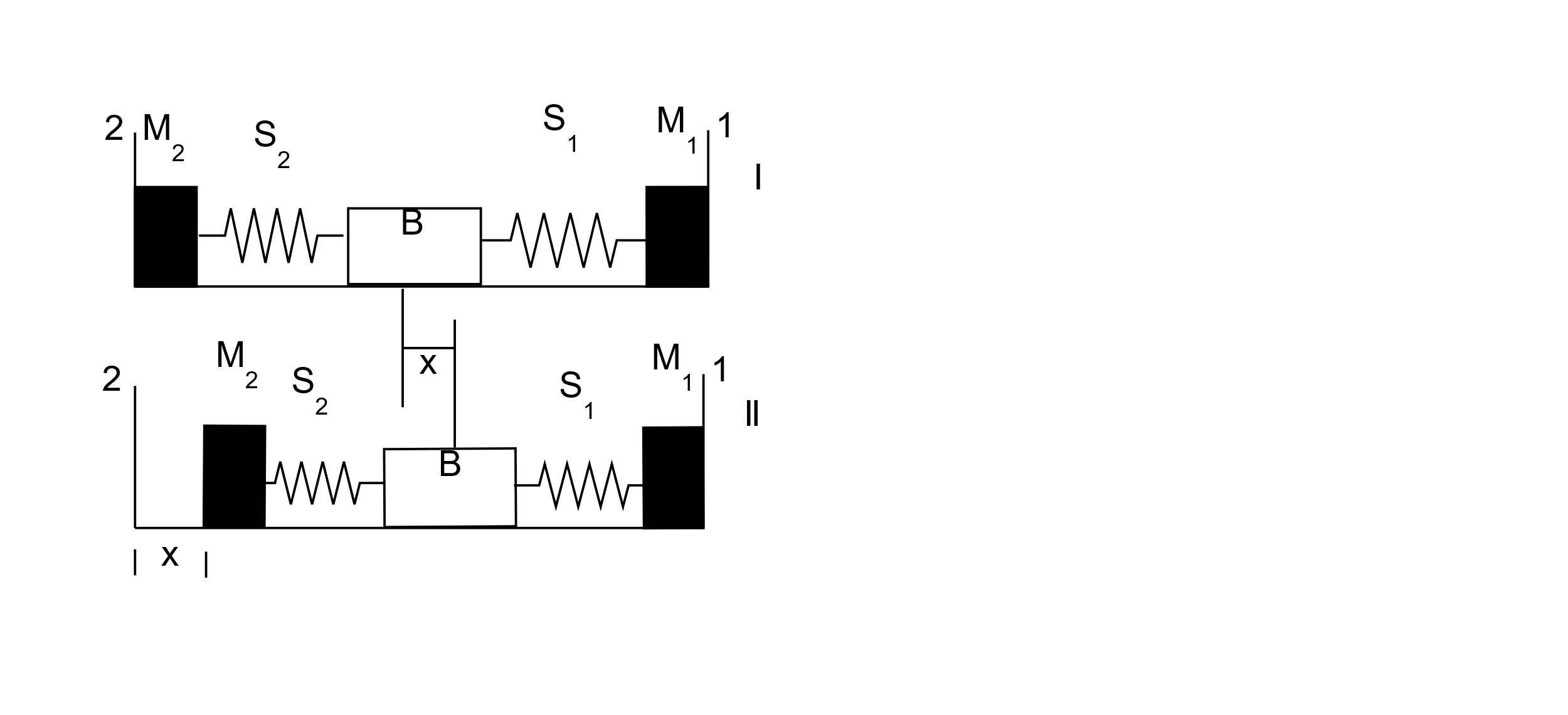
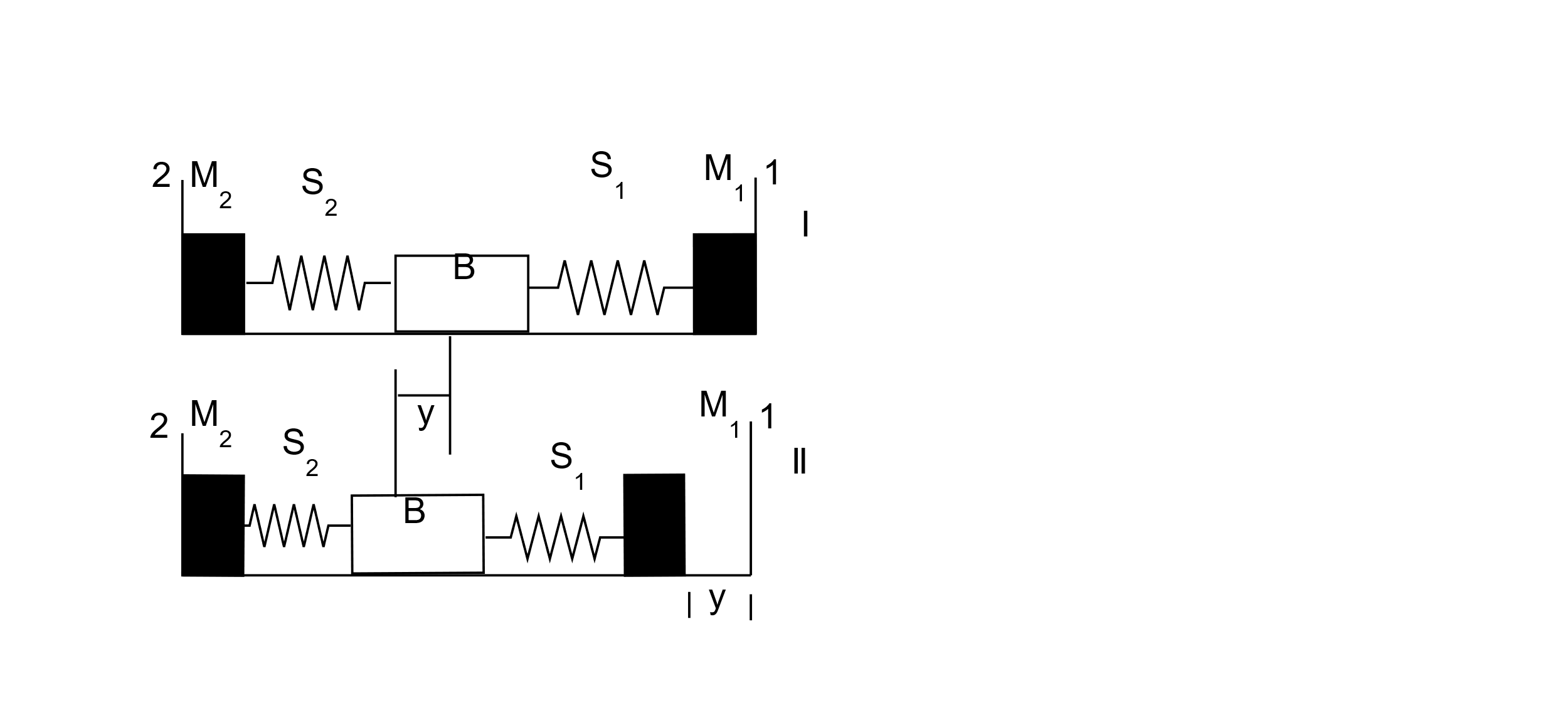
Now that we have the right diagrams with respect to the displacement x and y, we can move onto finding the ratio as asked. In order to do this, we need to establish a relationship so as to move forward. The velocity of the blocks is considered first, but the velocity of both cases is zero. Now we move onto potential energy of the spring
We can use the sum of kinetic energy and potential energy (total energy) here.
 $ P{E_X} + K{E_X} = P{E_y} + K{E_y} $
The kinetic energy of the springs are zero hence we arrive at,
 $ \dfrac{1}{2}k{x^2} + 0 = \dfrac{1}{2}k{y^2} + 0 $
But one of the spring constants (spring constant of the second displacement, y) is $ 4k $
Substituting that we get, $ \dfrac{1}{2}k{x^2} + 0 = \dfrac{1}{2}4k{y^2} + 0 $
We bring the like terms to one side and get $ \dfrac{{{y^2}}}{{{x^2}}} = \dfrac{1}{4} $
We can now take the square root of this equation to get the final answer as, $ \dfrac{y}{x} = \dfrac{1}{2} $
In conclusion, the right answer is option (C) $ \dfrac{1}{2} $ .

Note:
Spring constant or the force constant is derived by Hooke's law. Hooke's law, law of elasticity discovered by the English scientist Robert Hooke in 1660, states that, for relatively small deformations of an object, the displacement or size of the deformation is directly proportional to the deforming force or load.