Question

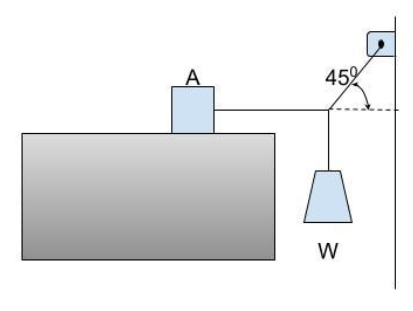
a. Block A as shown in figure, weighs 60.0N. The coefficient of static friction between the block and the surface on which it rests is 0.25. The weight w is 12.0N and the system is in equilibrium. Find the friction force exerted on block A .
b. Find the maximum weight w for which the system will remain in equilibrium.

Answer 1

Hint: In order to solve this problem one must be acquainted with the concept of resolution of forces and balancing of forces. If one is able to draw the free body diagrams(FBD) then that will be easier to solve the problem. To draw an FBD just cut the cable from the desired section and show the internal and external forces. Later on just resolve the force apply the conditions for equilibrium to find unknown focus.

Complete step by step answer:
To find the friction force on block A: To find the frictional force acting on block A we need to create a free body diagram and show all the forces acting on the desired section. The following figure shows the forces that are active in the system.

The tension in wire T attached to the hook has two components one balances the wt. W while other balance the friction force F
${\mathbf{Tsin}}\left( {45} \right) = {\mathbf{w}}$
${\mathbf{T}} = \dfrac{{\mathbf{w}}}{{\sin 45}}$……..(1)

The force due to static friction on block A is equal to the horizontal component of the
tension.
The expression for frictional force is,
${F_f} = {\mathbf{T}}\cos \left( {45} \right)$
Substitute ​ value of T from (1) in the above frictional force expression
${F_f} = \dfrac{{\mathbf{w}}}{{\sin 45}}\cos \left( {45} \right) = w\cot (45)$
${F_f} = 12\cot (45)$
${F_f} = 12N$
Therefore, the friction force exerted on block A is 12N.

To find the maximum wt. W:
For the system to remain in equilibrium force of friction should be equal to the weight w of the block. The frictional force is given by
${F_f} = {m_A}g{\mu _s}$
Here, mass of A, g is acceleration due to gravity and is coefficient of static friction.
Substitute 60 N for and 0.25 for
​${F_f} = 60 \times 0.25$
${F_f} = 15N$
The force of friction should be equal to the weight w of the block so the weight of the block is also 15 N. Therefore, maximum weight w for the system to remain in equilibrium is 15 N.

Hence, the correct answer is option (B).

Note: The component of force which is parallel or collinear to the side with which the resultant force is inclined at a particular angle should always be taken as the cosine component while the other component must be taken as sine component. This thumb rule will save a lot of time and will help in avoiding any type of confusion.