Question

A black body is at a temperature of \[5760{\text{ }}K.\] The energy of radiation emitted by the body at wavelength \[250nm\] is U1, at wavelength \[500nm\] is U2 and that at \[1000nm\] is U3. Wien's constant, \[b{\text{ }} = {\text{ }}2.88{\text{ }}X{\text{ }}{10^6}nmK.\] Which of the following is correct?
A. \[{U_1} = {\text{ }}0\]
B. \[{U_3} = {\text{ }}0\]
C. \[{U_1} > {\text{ }}{U_2}\]
D. \[{U_2} > {\text{ }}{U_1}\]

Answer 1

Hint: To solve this question, i.e., to check which option is correct. We will start with finding the maximum amount of emitted radiation corresponding to \[{\lambda _m}.\] Now, using that we will draw the graph and hence we will get the required answer.

Complete step by step answer:
We have been given that a black body is at a temperature of \[5760{\text{ }}K.\] The energy of radiation emitted by the body at wavelength \[250nm\] is U1, at wavelength \[500nm\] is U2 and that at \[1000nm\] is U3. Wien's constant, \[b{\text{ }} = {\text{ }}2.88{\text{ }}X{\text{ }}{10^6}nmK.\] We need to find which is correct.
We have been given the temperature \[ = {\text{ }}5760{\text{ }}K\]
We are also been given the energy of radiation emitted by the body at wavelength, \[{U_1} = {\text{ }}250{\text{ }}nm\], at wavelength, \[{U_2} = {\text{ }}500{\text{ }}nm\], at wavelength, \[{U_3} = {\text{ }}1000{\text{ }}nm\]
And also given the Wein constant, \[b{\text{ }} = {\text{ }}2.88{\text{ }}X{\text{ }}{10^6}nmK\]
We know that, the maximum amount of emitted radiation corresponding to \[{\lambda _m} = \frac{b}{T}\]
\[ \Rightarrow {\lambda _m} = \frac{{2.88 \times {{10}^6}nmK}}{{5760K}} = 500\;nm\] ​

Now if we draw graph from it, we get

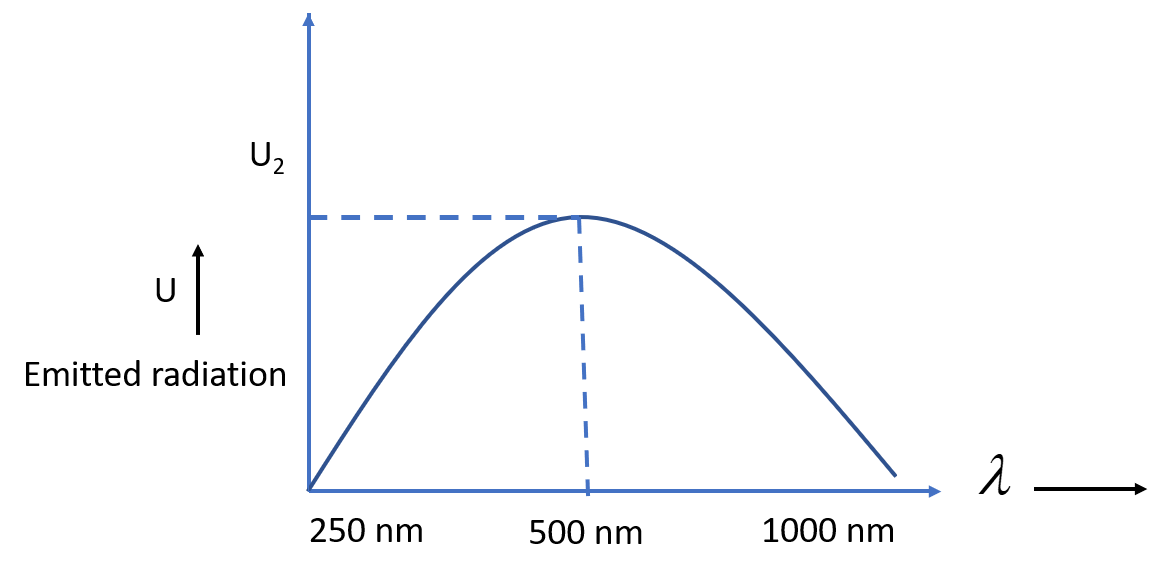
From the graph it is clear that, \[{U_2} > {\text{ }}{U_1}\] and \[{U_2}{\text{ < }}{U_3}\]
Now, let us check the options given to us.

Option A. \[{U_1} = {\text{ }}0,\] since, \[{U_1}\] is not equal to \[0,\] so, this option is incorrect.
Option B. \[{U_3} = {\text{ }}0,\] since, \[{U_3}\] is not equal to \[0,\] , so this option is incorrect.
Option C. \[{U_1} > {\text{ }}{U_2},\] since, \[{U_1}\] is not greater than \[{U_2},\] so, this option is incorrect.
Option D. \[{U_2} > {\text{ }}{U_1},{U_2}\] is greater than \[{U_1},\] so, this option is correct.

Note:In the question, we have been given about the Wien’s constant. Let us read about Wien constant. It is the product of the temperature of a black body in kelvin and the wavelength of its peak energy output in meters, is equal to Wien's constant. As the black body grows hotter, the wavelength of its peak energy grows shorter. Wien constant is denoted by b and is equals to \[2.88{\text{ }}x{\text{ }}{10^6}nmK.\]